The Floating Point Numbers System
Floating Point Format
Bits, Bites and Words
| base 10 | conversion | base 2 |
| 1 | $1=2^0$ | 0000 0001 |
| 2 | $2=2^1$ | 0000 0010 |
| 4 | $4=2^2$ | 0000 0100 |
| 8 | $8=2^3$ | 0000 1000 |
| 9 | $8+1=2^3+2^0$ | 0000 1001 |
| 10 | $8+2=2^3+2^1$ | 0000 1010 |
| 27 | $16+8+2+1=2^4+2^3+2^1+2^0$ | 0001 1011 |
Integers
The standard integer format is 16 bit, with range $$(-32768,32767)=(-2^{-15},2^{15}-1),$$ so that the 16bit word $$(b_{15}\dots b_0)_2$$ represents the integer $$b_{15}\cdot2^{15}+\dots+b_0\cdot2^0-2^{15}.$$ In MatLab, integers by default are stored as double-precision floating point. You can force using proper integer types to save memory, e.g.Single-precision floating-point numbers
IEEE 754 standard: Sign (1 bit), Exponent (8 bits), Mantissa (23+1 bits)The first bit of the mantissa is always equal to 1 and so not stored.
The 8 bit exponent range is $(-126,127)$, obtained from $(0,2^8-1)$ via a shift by $-127$ and reserving the exponents $-127$ (0 and denormalized numbers) and $128$ (Inf and NaN).
The 23 bit mantissa represents the binary number $(1.b_{22}\dots b_{0})_2$
Example:

Double-precision floating-point numbers
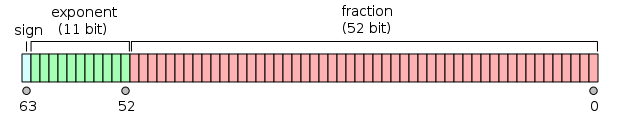
IEEE 754 standard: Sign (1 bit), Exponent (11 bits), Mantissa (52+1 bits)The first bit of the mantissa is always equal to 1 and so not stored.
The 11 bit exponent range is $(-1022,1023)$, obtained from $(0,2^{11}-1)$ via a shift by $-1023$ and reserving the exponents $-1023$ (0 and denormalized numbers) and $1024$ (Inf and NaN).
The 52 bit mantissa represents the binary number $(1.b_{51}\dots b_{0})_2$
Bits layout:
Significant decimal digits: 15 to 17.
Range: $(2^{-1023},2^{1024})\simeq(10^{-308},10^{308})$
Important General Facts
- When a number $x$ is stored in floating point format, it is rounded to
the nearest floating point number $\hat x=f(x)$.
Example: in single precision, $\frac{1}{3}=(0.\overline{01})_2$ is stored as $$(0.0101010101010101011)_2=\frac{11184811}{33554432}\simeq0.3333334.$$ - The machine precision $\epsilon$ is the smallest number such that $1+\epsilon>1$. Four single precision floating point arithmetic
$\epsilon=2^{-23}\simeq1.2\cdot10^{-7}$, for double precision
$\epsilon=2^{-52}\simeq2.2\cdot10^{-16}$. - This is also an upper bound for the largest relative rounding error, namely $$\frac{|\hat x-x|}{|x|}\leq\epsilon.$$
Floating Point Arithmetic
To confuse things, sometimes approximated expressions give, just by chance, the correct result, e.g.
the corresponding operations in floating point arithmetic,
e.g. $a\oplus b=fl\left(fl(a)+fl(b)\right)$.
We start with an interesting example: $3\odot\left(4\oslash3\ominus1\right)\ominus1=\epsilon_m$.
$$ 1\oslash3=1.\overbrace{01\dots01}^{22}1_2\cdot10_2^{-2} = 0.\overbrace{01\dots01}^{24}1_2 $$ $$ 4\oslash3 = 4\otimes(1\oslash3) = 1.\overbrace{01\dots01}^{22}1_2 $$ $$ 4\oslash3\ominus1 = 0.\overbrace{01\dots01}^{22}1_2 $$ $$ 3\otimes(4\oslash3\ominus1) = 0.\overbrace{10\dots10}^{20}11_2 + 0.\overbrace{01\dots01}^{20}011_2 = 1.\overbrace{0\dots0}^{22}1_2 $$ $$ 3\odot\left(4\oslash3\ominus1\right)\ominus1=0.\overbrace{0\dots0}^{22}1_2 = 2^{-23}=\epsilon_m $$
Propagation of Errors: multiplication/division
Assume that $fl(x)=x+\delta x$ and $fl(y)=y+\delta y$ and set $\epsilon_x=\frac{\delta x}{x}$, $\epsilon_y=\frac{\delta y}{y}$. Then, from Taylor series, $$ \frac{1}{y+\delta y} \simeq \frac{1}{y} - \frac{\delta y}{y^2} $$ so that it's enough to see what happens for multiplication. Since $$ \left|\frac{(x+\delta x)(y+\delta y)-xy}{xy}\right|=\left|\frac{\delta x}{x}+\frac{\delta y}{y}+\frac{\delta x}{x}\frac{\delta y}{y}\right| \leq \epsilon_x+\epsilon_y+\epsilon_x\epsilon_y $$ then $$ \epsilon_{xy}\simeq \epsilon_x+\epsilon_y $$Propagation of Errors: addition/subtraction
In this case a similar relation holds for absolute errors: $$ \delta(x\pm y) \leq \delta x + \delta y $$ which is bad news for the relative error: $$ \left|\frac{(x+\delta x)\pm(y+\delta y)-(x\pm y)}{x\pm y}\right|=\left|\frac{\delta x\pm \delta y}{x\pm y}\right|\leq \frac{x}{x\pm y}\epsilon_x + \frac{y}{x\pm y}\epsilon_y $$ When $x\pm y$ gets very small and $x$ (and $y$) do not, the relative error $\epsilon_{x\pm y}$ gets very big. Example: $x=1.001$, $\delta x=0.001$, $y=1.000$, $\delta y=0.001$, $$\epsilon_x\simeq\epsilon_y\simeq10^{-3}=0.1\%,$$ $$\epsilon_{x-y}=\frac{1.001}{10^{-3}}10^{-3}+\frac{1.000}{10^{-3}}10^{-3}\simeq2=200\%.$$IEEE Arithmetic
In general, in floating point arithmetic, if $a$ and $b$ are floating point numbers (namely here we are not considering the errors due to the roundoff of $a$ and $b$ themselves), $$ a\oplus b = (a+b)(1+\epsilon), \epsilon\leq\epsilon_m, $$ $$ a\ominus b = (a-b)(1+\epsilon), \epsilon\leq\epsilon_m, $$ $$ a\otimes b = (a\cdot b)(1+\epsilon), \epsilon\leq\epsilon_m, $$ $$ a\oslash b = \frac{a}{b}(1+\epsilon), \epsilon\leq\epsilon_m, $$An Elementary Application
Problem: Analyze the relative error in computing the smallest root $x_0$ of $$x^2-2x+\delta=0$$ for small $\delta>0$. Notice that $x_0>0$.Solution 1
Let us use first the formula $x_0=1-\sqrt{1-\delta}$ (for small $\delta$, $x_0\simeq\delta/2$), so $$fl(\sqrt{1-\delta})\simeq\sqrt{(1-\delta)(1+\epsilon_m)}(1+\epsilon_m)\simeq \sqrt{1-\delta}(1+3\epsilon_m/2),$$Then $\;\;\;fl(x_0)\simeq\left(1-\sqrt{1-\delta}(1+1.5\epsilon_m)\right)(1+\epsilon_m)$ and $$ |fl(x_0)-x_0|\simeq x_0\cdot\left|1.5\frac{\sqrt{1-\delta}}{x_0}\epsilon_m+\epsilon_m\right| $$ so that $$ \frac{|fl(x_0)-x_0|}{x_0}\simeq\frac{1.5\epsilon_m}{x_0}\simeq\frac{3\epsilon_m}{\delta}. $$ When $\delta$ gets very small, the relative error in $x_0$ gets very big!
Solution 2
Let us use now, instead, the mathematically equivalent expression $$x'_0=\frac{\delta}{1+\sqrt{1-\delta}}$$ Now $$ fl(x'_0)\simeq\frac{\delta}{(1+\sqrt{1-\delta}(1+1.5\epsilon_m))(1+\epsilon_m)}(1+\epsilon_m)\simeq\frac{\delta}{1+\sqrt{1-\delta}(1+2.5\epsilon_m)}(1+\epsilon_m) $$ so that $$ |fl(x'_0)-x'_0|\simeq \frac{4.5\epsilon_m\delta}{(1+\sqrt{1-\delta})(1+\sqrt{1-\delta}(1+2.5\epsilon_m))} $$ and $$ \frac{|fl(x'_0)-x'_0|}{x'_0}\simeq\frac{4.5\epsilon_m}{1+\sqrt{1-\delta}(1+2.5\epsilon_m)}\leq4.5\epsilon_m $$ Now the error does not diverge anymore!Problem
Is it more precise to evaluate $(a-b)^2$ via $$ (a,b)\to(a\ominus b)\to(a\ominus b)\otimes(a\ominus b) $$ or via $$ (a,b)\to(a\otimes a,a\otimes b,b\otimes b)\to (a\otimes a)\ominus 2(a\otimes b)\oplus(b\otimes b) $$ ?It depends on whether $a$ and $b$ are close or far. E.g. consider a decimal floating point system with two digits and take $a=1.8$ and $b=1.7$. Then $$ a\ominus b=0.1\;\hbox{ and }\;(a\ominus b)\otimes(a\ominus b)=0.01 $$ gives the exact solution while $$ (a\otimes a)\ominus 2(a\otimes b)\oplus(b\otimes b)=3.2-6.2+2.9=-0.10\; (!!!) $$ But, when $a=1.0$ and $b=0.05$, so that $(a-b)^2=0.9025$, $$ a\ominus b=1.0\;\hbox{ and }\;(a\ominus b)\otimes(a\ominus b)=1.0 $$ while $$ (a\otimes a)\ominus 2(a\otimes b)\oplus(b\otimes b)=1-0.10+0.0025=0.90 $$
Problem
Is it more precise to evaluate $a^2-b^2$ via $$ (a,b)\to(a\oplus b,a\ominus b)\to(a\oplus b)\otimes(a\ominus b) $$ or via $$ (a,b)\to(a\otimes a,b\otimes b)\to (a\otimes a)\ominus(b\otimes b) $$ ?As before, it depends on whether $a$ and $b$ are close or far.
E.g. consider again a decimal floating point system with two digits and take $a=1.8$ and $b=1.7$. Then $a\oplus b=3.5$ and $a\ominus b=0.1$, so $$ (a\oplus b)\otimes(a\ominus b)=0.35 $$ gives , as before, the exact solution while
$$ (a\otimes a)\ominus(b\otimes b)=3.2-2.9=0.30 $$ But for $a=1.0$ and $b=0.59$, so that $a^2-b^2=0.6519$, $$ a\oplus b=1.5, a\ominus b=0.5\;\hbox{ so that }\;(a\oplus b)\otimes(a\ominus b)=0.75 $$ while $$ (a\otimes a)\ominus(b\otimes b)=1.0-0.35=0.70 $$