Press ? for presentation controls.
Best viewed in Firefox,
Chrome and
Opera.
Numerical Methods
for PDE
General facts about PDEs
Examples of important elementary PDEs
| Poisson Equation | $u_{xx}+u_{yy}=f$ | $u$ = potential of a distribution of charges $f$ |
| Advection Equation | $u_{t}=c u_{x}$ | change of # of part. = flux of associated current |
| Waves Equation | $u_{tt}=u_{xx}+u_{yy}$ | evolution of mechanical and e.m. waves |
| Klein-Gordon Eq. | $u_{tt}=\alpha^2 u_{xx}-\mu^2u$ | evolution of a relativistic quantum particle |
| Sine-Gordon Equation | $u_{tt}=\alpha^2 u_{xx}-\mu^2\sin u$ | chains of pendula |
| Heat Equation | $u_{t}=\alpha^2\left(u_{xx}+u_{yy}\right)$ | evolution of heat in a media |
| Schrodinger Equation | $i u_{t}=\alpha^2\left(u_{xx}+u_{yy}\right)+V(x,y)u$ | evolution of a non-relativistic quantum particle |
Existence and uniqueness of solutions
Unlike ODEs, there are no general theorems about existence and uniqueness of PDEs solutions, even locally, except for the analytical case:
If $a(t,x,y)$, $b(t,x,y)$, $c(t,x,y)$ and $d(x,y)$ are analytical in all arguments, then the PDE $$ u_t = a u_x + b u_y +c\,,\;u(0,x,y) = d(x,y) $$ has a unique analytical solution for small enough $t$, $x$ and $y$.
This theorem though fails if any of the function is just simply smooth
rather than analytic!
see
https://en.wikipedia.org/wiki/Lewy's_example.
Classification
Consider a linear PDEs of 2nd order with constant coefficients $$ A u_{tt} + 2B u_{tx} + C u_{xx} + \hbox{lower order terms}=0 $$ We say this PDE is elliptic, hyperbolic or parabolic when, respectively, $AC-B^2>0$, $AC-B^2<0$ or $AC-B^2=0$.Basic examples:
| Elliptic | $u_{xx}+u_{yy}=0$ |
| Hyperbolic | $u_{tt}=u_{xx}$ |
| Parabolic | $u_{t}=u_{xx}$ |
Classification
More generally, loosely speaking:- Elliptic PDEs describe processes that have already reached a steady state, and so are time-independent.
- Hyperbolic PDEs describe time-dependent conservative processes, such as convection, thsat are not evolving towards a steady state.
- Parabolic PDEs describe time-dependent dissipative processes, such as diffusion, that are evolving towards a steady state.
Hyperbolic PDEs
Advection equation
Continuity equation
Consider a fluid of density $u(t,\vec x)$.Given any region $V$ bounded by a closed surface $\partial V$,
we have the following continuity equation
for the mass of fluid $M$ in $V$: $$ \frac{dM(t)}{dt} + \iint_{\partial V} u(t,\vec x)\,\vec v(t,\vec x)\cdot \vec{dS}(\vec x) = \Sigma(t), $$ where $\Sigma$ is the contribution given by sources and sinks inside $V$.
Advection equation
In absence of sources/sinks, we can use Stokes' theorem $$ \iint_{\partial V} \vec F\cdot \vec{dS} = \iiint_V \vec\nabla\cdot\vec F dV $$ to convert the integral continuity equation into its differential form: $$ \frac{\partial u}{\partial t} + \vec\nabla\cdot\left(u \vec v\right) = 0. $$ Finally, in case of an incompressible fluid (i.e. $\vec\nabla\cdot\vec v=0$)this equation reduces to the advection equation $$ \frac{\partial u}{\partial t} + \vec v \cdot \vec\nabla u = 0. $$
1D Advection equation
We consider in particular the simple case of a 1-dimensional fluid with constant velocity field $c$,in which case the advection equation reduces to $$ u_t=cu_x. $$ The most natural initial condition for such equation is specifying the shape of the solution at $t=0$, namely $u(0,\vec x)=f(\vec x)$.
Characteristics
The analytical solution of the advection equationcan be determined by the method of characteristics,
which in this cases reduces to the following observation. Re-write the PDE as $$ (\partial_t-c\partial_x) u(t,x) = 0,\; u(0,x)=f(x). $$ Hence $u$ is constant on the integral lines of the vector field $\partial_t-c\partial_x$.
In other words, the solution is $$ u(x,t) = f(x+ct), $$ namely the profile of the solution at time $t$ is the same
as the profile at the initial time shifted by $ct$ to the left.
Solving Advection PDE with FDM
Below we solve numerically the 1D advection equationwith several different instances of the Finite Differences Method
to test the weak and strong points of this method
for hyperbolic PDEs. Recall that the basic idea of this method is replacing
the "phase space" $[0,T]\times[0,L]$ with the uniform lattice
$$t_n = n\Delta t,\;0\leq n\leq N;\;\;x_m = m\Delta x,\;0\leq m\leq M$$
and $u_t$ and $u_x$ with one of their discrete approximations.
1. FTBS (Upwind Method)
In this first method, we use the forward Euler approximation for time derivatives and the backward one for space derivatives (Forward in Time, Backward in Space): $$u_t(t_n,x_m)\to\frac{u_{n+1,m}-u_{n,m}}{\Delta t}$$ $$u_x(t_n,x_m)\to\frac{u_{n,m}-u_{n,m-1}}{\Delta x}.$$ Then the PDE $u_t=cu_x$ becomes the linear system $$ u_{n+1,m} = u_{n,m} + \nu\left(u_{n,m}-u_{n,m-1}\right)\,, $$ with $1\leq n\leq N-1$, $1\leq m\leq M$, $\nu=\frac{c\Delta t}{\Delta x}$.FTBS Diagram
This scheme can be summarized by the following diagram: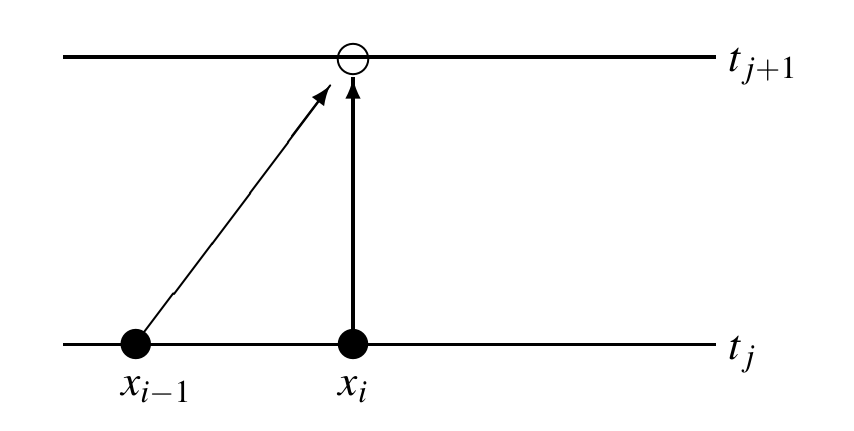
FTBS Initial Conditions
The initial condition of the Advection PDE $u(0,x)=f(x)$ becomes here the vector $$ u_{_{0,0}}=f(0),\dots,u_{_{0,m}}=f(x_m),\dots,u_{_{0,M}}=f(L). $$ Notice that the solution of FTBS system cannot givethe values of the $u_{n,0}$, $n\geq1$,
since they would involve the coefficients $u_{n-1,-1}$!
FTBS Initial Conditions
This is due to the fact that the PDE is defined for all $x\in\Bbb R$ but numerical methods can only solve the problem within a finite box. The impossibility to get the $u_{n,0}$, $n\geq1$, corresponds to the fact that the characteristics of the PDE hit the boundary at all points $(t,0)$. We need therefore to provide an extra boundary condition on the segment $(t,x)$, $0\leq x\leq L$, corresponding to the values reached, on that segment, by the solution of the PDE. Remark: different schemes will entail different kinds of extra boundary conditions!Implementation in Python
Method convergence: The CFL condition
Courant, Friedrichs and Lewy formulated a simple necessary condition for the convergence of a finite difference scheme. For any variable $u_{n,m}$, all points that influence its value in the FTBS system form a triangle, as in the example below: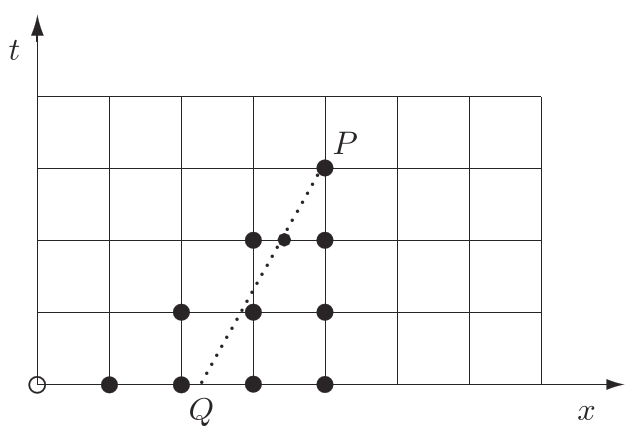
The CFL condition
The triangle is called domain of dependence of $u_{n,m}$. The picture also shows the characteristic linepassing through the point $(n,m)$ of the lattice.
In order for the scheme to converge to the exact solution, the characteristic must be inside the domain of dependence. Otherwise, indeed, changes made to the initial condition close to where the characteristic meets the $x$ axis would not influence $u_{n,m}$!
The CFL condition
Recall that characteristics for the Advection PDE are $x(t) = x_0-ct$,so, in case of the FTBS scheme,
there cannot be convergence for $c>0$
while, for $c<0$, we must also have
$|1/c|\leq\Delta t/\Delta x$,
namely $|\nu|\leq1$. Remark: the CFL condition is necessary but not sufficient!
Method convergence: The von Neumann condition
Consider a solution of the form $u_{n,m} = \lambda^n e^{ikm\Delta x}$ (Fourier mode). Then $\;\;\;\lambda^{n+1} e^{ikm\Delta x} = (1+\nu)\lambda^n e^{ikm\Delta x} - \nu\lambda^n e^{ik(m-1)\Delta x}$, namely $\lambda = 1+\nu - \nu e^{-ik\Delta x}$. This means that FTBS is stable when $$ |\lambda|^2 = 1 + 4\nu(1+\nu)\sin^2\frac{k\Delta x}{2}\geq1, $$ in particular when $-1\leq\nu\leq0$.We say that this method is conditionally stable.
2. FTCS
Switching the space derivative from Backward to Forward clearly cannot not fix the problem above,it just switches the sign for which the method is stable. It is tempty to come up with a method conditionally stable for both signs of $c$ by using instead "centered in space" derivatives, namely $$u_x(t_n,x_m)\to\frac{u_{n,m+1}-u_{n,m-1}}{2\Delta x}.$$ The advection PDE $u_t=cu_x$ becomes now the linear system $$ u_{n+1,m} = u_{n,m} + \frac{\nu}{2}\left(u_{n,m+1}-u_{n,m-1}\right)\,, $$ with $0\leq n\leq N$, $1\leq j\leq M-1$, $\nu=\frac{c\Delta t}{\Delta x}$.
FTCS Diagram
This scheme can be summarized by the following diagram: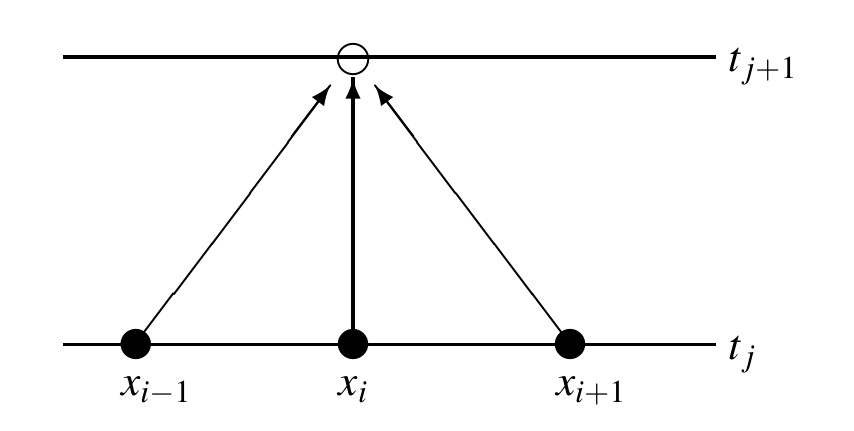
FTCS vc FTBS
Notice that in this case we need to set boundary conditions at both $x=0$ and $x=L$. As expected, here the domain of dependence of $u_{n,m}$ is a triangle that is symmetric with respect to the vertical direction and therefore we get a weaker bound from the CFL condition: with both positive or negative values of $c$ we have that the characteristics are inside the domain of dependence as long as $|\nu|\leq1$. The von Neumann condition though gives us that $$|\lambda|^2=1+\nu^2\sin^2(k\Delta x)$$ so this method turns out to be unconditionally unstable,namely unstable for any value of $c$!
3. The Lax Method
It turns out that there is a simple way to fix this problem, namelyreplacing the $u_{n,m}$ term in the FTCS system
with the average over its two neighbours: $$ u_{n+1,m} = \frac{u_{n,m+1}+u_{n,m-1}}{2} + \nu\frac{u_{n,m+1}-u_{n,m-1}}{2}\,. $$
Lax Diagram
This scheme can be summarized by the following diagram: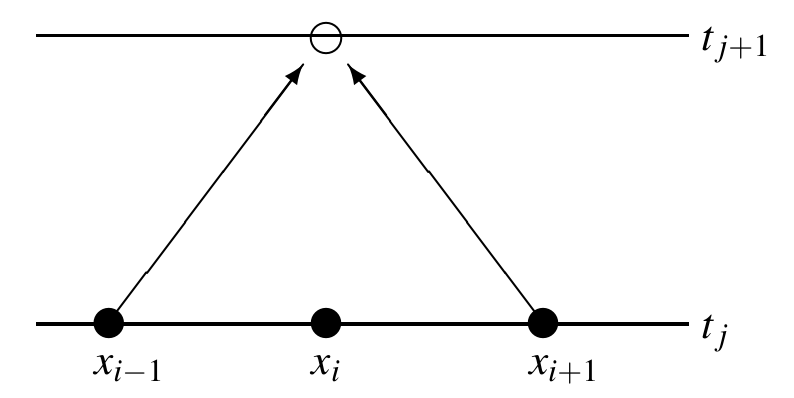
Lax's CFL and Von Neumann conditions
The CFL condition for this case, as expected, holds for both positive and negative values of $c$ as long as $\nu$\leq1. Moreover, in this case $$ |\lambda|^2 = 1-(1-\nu^2)\sin^2(k\Delta x) $$ so we get also stability as long as $\nu^2\leq1$.General properties of numerical pde methods
Consistency, stability, convergence
After sdiscussing the behavior of some PDE numerical methods, let us state some important definitions and an important theorem.A method is:
- Consistent if its truncation error (i.e. the local error) goes to zero as $\Delta t,\Delta x\to0$.
- Stable if the operator $T$ sending initial conditions to the corresponding numerical solutions is bounded, namely there are no initial conditions on which the numerical solution diverges (von Neumann analysis).
- Convergent if the global error goes to zero as $\Delta t,\Delta x\to0$.
The Lax Equivalence Theorem
For a consistent difference approximationto a well-posed linear evolutionary problem,
the stability of the scheme is equivalent to its convergence.
Parabolic PDEs
Diffusion equation
Just as the advection PDE, also the heat PDEcomes from the continuity equation $$ \frac{\partial u}{\partial t} + \vec\nabla\cdot\vec j = 0. $$ The difference is that here we do not consider a fluid, where $\vec j=u\vec v$, but rather some diffusing material that follows Fick's law, namely $\vec j(t,\vec x) = -K(u(t,\vec x),\vec x)\vec\nabla u(t,\vec x)$, where the function $K$ is the diffusion coefficient. The resulting PDE is called Diffusion Equation: $$ u_t = \vec \nabla\cdot (K\nabla u). $$
Heat equation
When the diffusion coefficient is constant,the equation is called heat PDE $$ u_t = K\Delta u, $$ where $\Delta$ is the Laplacian operator, namely $$ \Delta u(x^1,\dots,x^n) = u_{x^1x^1}+\dots+u_{x^nx^n}. $$
1D Heat equation
In 1+1 dimensions, the heat PDE writes $$ u_t=c\,u_{xx}\,,\;u(0,x)=f(x)\,. $$ We consider Dirichlet boundary conditions $u(t,0)=u(t,1)=0.$ Physically, this corresponds to heating a wirewith some initial temperature distribution $f(x)$
while keeping the end-points at some fixed temperature. The solution of the PDE
will give the evolution of the temperature as $t\to\infty$.
1. FTCS
$u_{xx}(t_n,x_j)\to\frac{u_{n,j+1}-2u_{n,j}+u_{n,j-1}}{\left(\Delta x\right)^2}$
so the equation translates into
$$ u_{n+1,j} = u_{n,j} + \nu\left(u_{n,j+1}-2u_{n,j}-u_{n,j-1}\right)\,, $$
where $\nu=\frac{c\Delta t}{\left(\Delta x\right)^2}$
(implemented in p2a.m )
FTCS Stability
As for the hyperbolic case, we consider the solution $u(t,x) = e^{ik(x-c t)}$, so that $$ u_{n,j} = e^{ik(j\Delta x-c n\Delta t)} = G(k)^n e^{ikj\Delta x}\,, $$ and we plug it into the system, so that we get $$ G(k)^{n+1} e^{ikj\Delta x} = G(k)^{n} e^{ikj\Delta x} + \nu\left(G(k)^{n} e^{ik(j+1)\Delta x} - 2G(k)^{n} e^{ikj\Delta x} + G(k)^{n} e^{ik(j-1)\Delta x}\right)\,, $$ namely $$ G(k) = 1 - \nu(2\cos\left(k\Delta x\right)-2) = 1 - 4\nu\sin^2\frac{k\Delta x}{2} $$so a necessary condition for the stability of this method is $$\nu=\frac{c\Delta t}{(\Delta x)^2}\leq\frac{1}{2}$$
FTCS accuracy problem
The FTCS method has a big problem: in order to keep it stable, if we decrease $\Delta x$ by a factor $h$we need to decrease at the same time $\Delta t$ by a factor $h^2$,
which leads to unreasonably small values of $\Delta t$
when a large accuracy is needed.
Implementation in MATLAB
2. CTCS (Richardson Method)
One can try using central derivative approx for time: $$ u_t(t_n,x_j)\to\frac{u_{n+1,j}-u_{n-1,j}}{2\Delta t}. $$ Then the system becomes $$ u_{n+1,j} = u_{n-1,j} + 2\nu\left(u_{n,j+1}-2u_{n,j}-u_{n,j-1}\right)\,. $$ but the vN analysis shows that the ampl. factor $G(k)$ satisfies $$ g^2+2\beta g-1,\;\;\beta=4\nu\sin^2\frac{k\Delta x}{2} $$ which has a solution with modulus larger than 1 for all $\nu$,namely this method is unconditionally unstable.
3. DuFort-Frankel method
Similarly to how we did for the advection equation, one can tryreplacing the $u_{n,j}$ term with its time average: $$ u_{n+1,j} = u_{n-1,j} + 2\nu\left(u_{n,j+1}-(u_{n+1,j}+u_{n-1,j})+u_{n,j-1}\right)\,, $$ so that $$u_{n+1,j}=\frac{1-2\nu}{1+2\nu}u_{n-1,j}+2\frac{\nu}{1+2\nu}\left(u_{n,j+1}+u_{n,j-1}\right).$$ Now $G(k)$ solves $$ (1+2\nu)g^2+4g\nu\cos(k\Delta x)+2\nu-1=0\, $$ whose roots are all outside of the unit disk for all $\nu$,
namely this method is unconditionally stable!
3. DuFort-Frankel method
Does this method converge to the exact solution? Actually not!Indeed, while it is stable, it is not consistent. We can verify this with Taylor expansion.
Write just $u_t$, $u_x$ and so for the values of those functions at $(t_n,x_j)$. Then: $$ u_{n+1,j}-u_{n,j} = u_t \Delta t + O(\Delta t^3), $$ $$ u_{n,j+1}-(u_{n+1,j}+u_{n-1,j})+u_{n,j-1} = u_{xx}\Delta x^2 - u_{tt}\Delta t^2 + O(\Delta x^4,\Delta t^4) $$ and so the DuFort-Frankel method system is equivalent to $$ u_t = c u_{xx} - c \frac{\Delta t^2}{\Delta x^2} u_{tt} + O(\Delta x^2,\Delta t^2,\Delta t^4/\Delta x^2). $$
3. DuFort-Frankel method
This shows that this method is not consistent for all choices of $\Delta t,\Delta x\to0$. For instance, if we choose $\Delta t=\Delta x=h$, then the numerical solutions of the DuFort-Frankel method actually converge,for $h\to0$, to the solutions of the hyperbolic PDE $$ u_t = c ( u_{xx} - u_{tt} )\;\;! $$
4. BTCS method
Often implicit methods fix many problems, so one can try replacing the time derivative with its backward in time expression: $$u_t(t_n,x_j)\to\frac{u_{n,j}-u_{n-1,j}}{\Delta t}$$ The system now becomes$$ u_{n,j} = u_{n-1,j} + \nu\left(u_{n,j+1}-2u_{n,j}+u_{n,j-1}\right)\,, $$
that can be solved "backwards":
$$ u_{n-1,j} = u_{n,j} - \nu\left(u_{n,j+1}-2u_{n,j}+u_{n,j-1}\right)\,, $$
4. BTCS Solution
Namely, $\vec u_{n-1}$, the vector of values of $u$ at $t=t_{n-1}$, is equal to $M\vec u_{n}$,
where the matrix $M$ is tridiagonal with $1+2\nu$ on the diagonal
and $-\nu$ in the upper/lower diagonal terms.
Hence
$\vec u_{n} = (M^{-1})^n\cdot\vec u_{0}$
(implemented in p2b.m )
4. BTCS - Stability
Here we get $$ G(k)^{n+1} e^{ikj\Delta x} = G(k)^{n} e^{ikj\Delta x} + \nu\left(G(k)^{n+1} e^{ik(j+1)\Delta x} - 2G(k)^{n+1} e^{ikj\Delta x} + G(k)^{n+1} e^{ik(j-1)\Delta x}\right)\,, $$ namely $$ G(k) = 1 - \nu\,G(k)(2\cos\left(k\Delta x\right)-2) $$so that $$ G(k) = \frac{1}{1+4\nu\sin^2\frac{k\Delta x}{2}} $$
This method therefore is stable for all $\Delta t$ and $\Delta x$!
4. BTCS - Weak point
Via Taylor series analysis, we see that the BTCS system is equivalent to $$ u_t = c u_{xx} + O(\Delta t,\Delta x^2). $$ Just as with FTCS, being only order 1 in time is a problem when you want a reasonably small error in your numerical solution.Next method is a way to fix this situation.
Implementation in MATLAB
5. Crank-Nicholson method
Replace the CS r.h.s. with its forward average in time:$u_{xx}(t_n,x_j)\to \frac{u_{n+1,j+1}-2u_{n+1,j}+u_{n+1,j-1}}{\left(\Delta x\right)^2} + \frac{u_{n,j+1}-2u_{n,j}+u_{n,j-1}}{\left(\Delta x\right)^2}$
The Heat equation now translates into $$ -\nu u_{n+1,j+1}+2(1+\nu)u_{n+1,j}-\nu u_{n+1,j-1} = \nu u_{n,j+1}+2(1-\nu)u_{n,j}+\nu u_{n,j-1} $$
which writes as $M\vec u_{n+1}=N\vec u_{n}$
for two tridiagonal matrices $M,N$,
so that
$\vec u_{n} = (M^{-1}N)^n\cdot\vec u_{0}$
5. Crank-Nicholson Stability
$$ G(k) = \frac{1-2r\sin^2\frac{k\Delta x}{2}}{1+2r\sin^2\frac{k\Delta x}{2}} $$
This method therefore is also unconditionally stable
plus
is 2nd order in both time and space.
Implementation in MATLAB
Elliptic PDEs
Poisson Equation
The most elementary Elliptic PDE,$$ u_{xx} + u_{yy} = \rho\;\;\hbox{ in }S\,,\;\;u|_{\partial S}=f, $$
is named Poisson Equation or, when $f=0$, Laplace Equation.
Example: electrostatic electric potential
In case of static electric fields, the two Maxwell's laws
$$ \vec\nabla\cdot\vec E = \frac{\rho}{\varepsilon} \,,\;\; \vec\nabla\times\vec E = -\frac{\partial\vec B}{\partial t}\,, $$
amount to
$$ \vec E=-\vec\nabla V \,,\;\; \Delta V=-\frac{\rho}{\varepsilon}\,, $$
where $V$ is the electric potential function
associated to the (conservative) electric vector field $\vec E$.
Electric Potential of a point-like charge
generated by a point charge $q=4\pi\varepsilon$, namely $$ \Delta V(x,y) = 4\pi\delta(x-0.5,y-0.5) $$ for all $(x,y)$ in $S=[0,1]\times[0,1]$. Usually the potential $V$ is set to zero at infinity
and the solution is the well known
potential of a charged point-like particle: $$ V = \frac{1}{r}. $$ Below we will simply set $V=0$ on the boundary of $S$.
Finite Differences -- Explicit method
$V_{xx}(x_i,y_j)\to\frac{V_{i+1,j}-2V_{i,j}+V_{i-1,j}}{\left(\Delta x\right)^2}$, $V_{yy}(x_i,y_j)\to\frac{V_{i,j+1}-2V_{i,j}+V_{i,j-1}}{\left(\Delta y\right)^2}$,
so that the equation translates into
$ \frac{V_{i+1,j}-2V_{i,j}+V_{i-1,j}}{\left(\Delta x\right)^2} + \frac{V_{i,j+1}-2V_{i,j}+V_{i,j-1}}{\left(\Delta y\right)^2} = 4\pi\rho_{i,j} \;,\;\; 1\leq i,j\leq N $
where $\rho_{i,j}$ is equal to 1 at $(N/2,N/2)$ and zero everywhere else.
Finite Differences -- Explicit method
by the 5-points stencil diagram below:
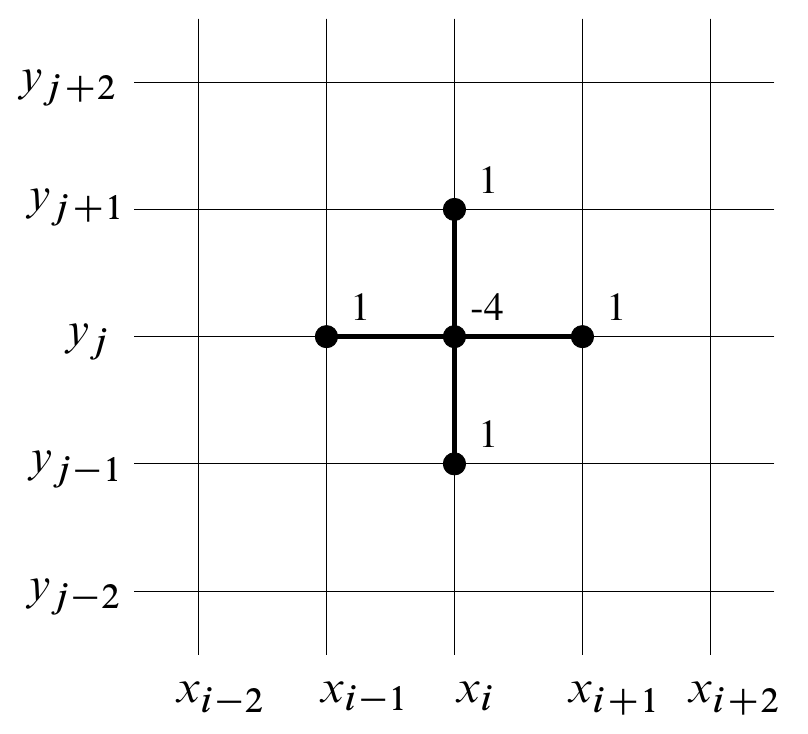
Finite Differences -- Explicit method
In matrix notation, sorting the $V_{i,j}$ in lexicografic order, this system writes as $M\vec V=\vec R$, where$$ M = \begin{pmatrix} B&-I&&&&&0\\ -I& B&-I&&&&\\ &.&.&.&&&\\ &&.&.&.&&\\ &&&.&.&.&\\ &&&&-I&B&-I\\ 0&&&&&-I&B\\ \end{pmatrix} $$
is a $N^2$ block matrix, where...
Finite Differences -- Explicit method
$$ B = \begin{pmatrix} 4&-1&&&&&0\\ -1& 4&-1&&&&\\ &.&.&.&&&\\ &&.&.&.&&\\ &&&.&.&.&\\ &&&&-1&4&-1\\ 0&&&&&-1&4\\ \end{pmatrix} $$
Local Truncation Error
Let $u(x,y)$ be the exact solution of the Poisson equation $\Delta u=f$ and denote by $\vec U$ the vector of all $u(x_i,y_j)$ in lexicographic order. The vector $\;\;\vec\tau = M\vec U-\vec R\;\;$, whose components are $ \tau_{i,j}=\frac{u(x_{i-1},y_j)+u(x_{i+1},y_j)+u(x_{i},y_{j-1})+u(x_{i},y_{j+1})-4u(x_i,y_j)}{h^2}-f(x_i,y_j)\,, $ represents the local truncation error for the 5-points stencil method. Via Taylor expansion we see that $$ \tau_{i,j}=\frac{h^2}{12}\left[u_{xxxx}(x_i,y_j)+u_{yyyy}(x_i,y_j)\right]+O(h^4) $$Global Error
Let $\vec u = \hat u_{i,j}$ be the solution of the system $M\vec u=\vec R$. Then $$\vec E= \vec U-\vec u$$ is the global error of the method. This vector satisfies the equation $$ M\vec E = M\vec U-M\vec u = \vec\tau +\vec R - \vec R = \vec\tau\,, $$ namely $$ \vec E = M^{-1}\vec\tau\,. $$Stability and Accuracy
Recall that the numerical solution of the Poisson equation through this method is $$\vec u = M^{-1}\vec R$$ and that $\vec R$ is determined by the boundary conditions. In particular, the method is stable if the norm of the inverse stays bounded for $h\to0$. As a byproduct, if a method is stable then the global erroris of the same order as the local one. Remark: all norms are equivalent in finite dimension,
so this fact can be verified in the most convenient one.
Stability and Accuracy
In this case it is convenient using the spectral norm. Since $M$ is symmetric, its spectral norm is just its largest eigenvalue in modulus and the norm of $M^{-1}$ is the inverse of the smallest eigenvalue in modulus of $M$. Hence it is enough to show that the spectrum of $M$ stays far from the origin as $h\to0$. A direct calculation shows that the eigenvectors of $M$ are the $ u_{i,j}^{p.q} = \sin(p\pi i h)\sin(q\pi jh),\;\;\;\;p,q=1,\dots,m $ with eigenvalues $ \lambda_{p,q} = \frac{2}{h^2}\left[\cos(p\pi h)-1+\cos(q\pi h)-1\right]. $Stability and Accuracy
The smallest in modulus of these eigenvalues is $ \lambda_{1,1} = \frac{2}{h^2}\left[\cos(\pi h)-1+\cos(\pi h)-1\right] \simeq -2\pi^2 + O(h^2), $ so that $$ \|M^{-1}\|_{sp} = \frac{1}{-2\pi^2 + O(h^2)} = -\frac{1}{2\pi^2} + O(h^2), $$ namely $M^{-1}$ is bounded in some nbhd of $h=0$.Evaluating in concrete a numerical solution
We showed above that the 5-points stencil method has local and global order $4$ in $\Delta x=\Delta y=h$. Finding the actual numerical solution to the Poisson equation $\Delta u=f$ amounts to solving the linear system $$ M\vec u=\vec R\,. $$ At this point, the PDE problem has become a linear algebra numerical problem. Methods to solve numerically linear systems can be found in any numerical anaysis introductory textbook.You can find a short introduction to this topic in these slides. Below we briefly discuss a few of these methods.
Solving $M\vec V=\vec R$ -- LU method
Write $M=LU$, with $L$ lower and $U$ upper triangular. $LU\vec V=\vec R$ can be easily solved by forward and backward substitutions.The complexity of this method is $O\left(N^3\right)$. For banded matrices of bandwidth $d$, the complexity goes down to $O\left(d^2N\right)$.
Solving $M\vec V=\vec R$ -- Jacobi method
with $D$ diagonal, $U$ upper and $L$ lower diagonal.
The solution is obtained iteratively by
$$ \vec V_{k+1} = -D^{-1}(L+U)\vec V_{k} + D^{-1}\vec R $$
This converges to the solution
iff the spectral radius of $D^{-1}(L+U)$ is $<1$.
This happens, for example, for diagonally dominant matrices.
First Implementation in Python
Second Implementation in Python
Solving $M\vec V=\vec R$ -- Gauss-Seidel method
with $D$ diagonal, $U$ upper and $L$ lower diagonal.
The solution is obtained iteratively by
$$ \vec V_{k+1} = -(L+D)^{-1}U\vec V_{k} + (L+D)^{-1}\vec R $$
The GS method converges when $M$ is symmetric or diagonally dominant. For tridiagonal matrices, it is equivalent to Jacobi.
Solving $M\vec V=\vec R$ -- GS with SOR relaxation
with $D$ diagonal, $U$ upper and $L$ lower diagonal.
The solution is obtained iteratively by
$$ \vec V_{k+1} = -(D+\omega L)^{-1}((1-\omega)D-\omega U)\vec V_{k} + (D+\omega L)^{-1}\vec R $$
where $0 < \omega < 2$
(it is sufficient for the convergence that $A$ is symmetric and positive-definite).
In general, the optimal $\omega$ depends on the boundary conditions.
The idea behind the
Finite Elements Method
A Linear system
Consider a finite dimensional vector space $V$ with a scalar product $\langle,\rangle$,a linear operator $A:V\to V$ and a vector $r\in V$.
We want to solve the equation $$ A v = r\,. $$
Recall that every finite dimensional vector space admits bases $\{e_1,\dots,e_n\}$, $n=\dim V$,
so that every $v\in V$ can be written in a unique way as $$v=\sum_{i=1}^n v_i e_i\,.$$
An equivalent formulation
Clearly a vector that is orthogonal to all $e_i$ must be zero (prove it!),so $Av=r$ is equivalent to the equation
$\langle A v,e_i\rangle = \langle r,e_i\rangle\,$, for all $1\leq i\leq n$.
An equivalent formulation
In turn, this is the same as asking
$\langle A v,s\rangle = \langle r,s\rangle\,$, for all $s\in V$.
While in finite dimension these two formulations are equivalent,
in infinite dimension
the latter is weaker,
namely it has in principle more solutions than the original one.
Example 1 -- ODEs
Consider the space $V=C^\infty[0,1]$ of all functions $u:[0,1]\to\Bbb R$ that are continuous on the whole $D=[0,1]$together with their derivatives of any order. $V$ is a vector space since, if $u,v\in V$, then also any linear combination $\alpha u+\beta v\in V$ for every $\alpha,\beta\in\Bbb R$.
The dimension of this space, though is infinite! For example $$ s_n(x) = \sin(2\pi n x)\,,\;c_n(x)=\cos(2\pi n x)\,,\; n=1,2,3,\dots $$ is a set of infinitely many linearly independent elements of $V$. In fact, every function in $V$ can be developed in Fourier series: $$ u=\sum_{n=1}^\infty \left(u_{s,n} s_n+u_{c,n} c_n\right) $$
The completion of $V$ with respect to $\langle,\rangle$ is called $L^2[0,1]$ and is the space of all measurable functions $u$ such that $$\|u\|^2=\int_0^1|u(x)|^2 dx<\infty\,.$$
$$ -u''(x)+r(x)u(x)=f(x)\,,\;x\in[0,1]\,,\;\;u(0)=u(1)=0\,, $$
with $f,r\in V$. This is a linear equation in $V$ and can be written as $$ Au=f\,,\;u\in C^\infty_0[0,1] $$ where $A$ is the linear operator from $V$ to itself $$ -\frac{d^2}{dx^2}+r(x) $$ and $C^\infty_0[0,1]$ is the subset of smooth functions that are zero at $x=0,1$.
First we take the scalar product with a $s\in C^\infty_0[0,1]$, so we get $$ -\langle u'',s\rangle + \langle r\cdot u, s\rangle = \langle f,s\rangle\,. $$ Then we integrate by parts the first term: $$ \langle u'',s\rangle = \displaystyle\int_0^1\!\!\!u''(x)s(x)dx = u'(x)s(x)\bigg|^1_0 - \displaystyle\int_0^1\!\!\!u'(x)s'(x)dx\,, $$ The equation now is $$ \langle u',s'\rangle + \langle r\cdot u, s\rangle = \langle f,s\rangle\,,\;\hbox{ for all }s\in C^\infty_0[0,1] $$
In this equation all functions appear under integral sign,
so there is no actual need to require
so much regularity:
it is enough to ask that both $u$ and $s$ belong to $H^1_0[0,1]$,
the space
of square-integrable functions whose first derivative
is also square-integrable and that converge
to $0$ for $x\to0^+,1^-$.
Approximating weak solutions
If $\{\phi_i\}$ is a basis for the subspace $H^1_0[0,1]$ of all functions of $L^2[0,1]$ with square-integrble gradient and which tend zero for $x\to0^+$ and $x\to1^-$, then
$\langle u',\phi'_i\rangle+r\langle u,\phi_i\rangle=\langle f,\phi_i\rangle$
for all $i$. Since $u=\sum_{i=1}^\infty u_i\phi_i$ and $f=\sum_{i=1}^\infty f_i\phi_i$ we have that
$\sum_{j=1}^\infty u_j\left( \langle \phi'_j,\phi'_i\rangle + r\langle \phi_j,\phi_i\rangle\right) = \sum_{j=1}^\infty f_j\langle \phi_j,\phi_i\rangle$
By truncating this sum to some $N$, we get that $$ AU=F $$ form some matrix $A$ and $F$.
Example 2 -- PDEs
Consider the space $V=C^\infty(S)$, where $S$ is the unit square $[0,1]\times[0,1]$, of all functions $u:S\to\Bbb R$ that are continuous on the whole square together with their derivatives of any order.Again, $V$ is an infinite dimensional vector space with scalar product
$$ \langle f,g \rangle = \displaystyle\iint_S\!\!\!f(x,y)g(x,y)dxdy\,. $$
$$ -u_{xx}(x,y)-u_{yy}(x,y)=f(x,y)\,,\;x\in[0,1]\,,\;\;u=0 on \partial S\,, $$ where $f\in V$ and $\partial S$ is the boundary of $S$.
This is a linear equation in $V$ and can be written as $$ Au=f\,,\;u\in C^\infty_0(S) $$ where $A$ is the linear operator from $V$ to itself $$ -(\partial_{xx}+\partial_{yy}) $$ and $C^\infty_0(S)$ is the subset of smooth functions that are zero at the boundary of $S$.
Then we integrate by parts the lhs terms as above: $$ \langle u_{xx},s\rangle = -\langle u_x,s_x\rangle\,,\;\langle u_{yy},s\rangle = -\langle u_y,s_y\rangle $$ The equation now is
$$ \langle\nabla u,\nabla s\rangle = \langle f,s\rangle\,,\;\hbox{ for all }s\in C^\infty_0(S) $$
Again, in this equation all functions appear under integral sign so there is no actual need to require so much regularity: it is enough to ask that both $u$ and $s$ belong to $H^1_0(S)$, the space of $L^2$ functions on $D$ whose gradient is also $L^2$ and that converge to 0 on any sequence of points converging to the boundary.
Approximating weak solutions
If $\{\phi_i\}$ is a basis for $H^1_0(S)$, then
$\langle \nabla u,\nabla \phi_i\rangle=\langle f,\phi_i\rangle$
for all $i$. Since $u=\sum_{i=1}^\infty u_i\phi_i$ and $f=\sum_{i=1}^\infty f_i\phi_i$ we have that
$\sum_{j=1}^\infty u_j \langle \nabla \phi_j,\nabla\phi_i\rangle = \sum_{j=1}^\infty f_j\langle\phi_j,\phi_i\rangle$
By truncating this sum to some $N$, we get that $$ AU=F $$ form some matrix $A$ and $F$.
Implementation of the
Finite Elements Method
Why FEM?
The main goal of the Finite Elements Method is having a method able to work on a domain $D$ no matter how complicated is its shape, bypassing the Finite Difference limitation to rectangular grids.This is accomplished mainly with the following two points:
- Generating a suitable mesh (possibly tailored on the specifics of the PDE) of $D$ with $N$ nodes
$\{p_1,\dots,p_N\}$ and a corresponding set of functions $\{\phi_1,\dots,\phi_N\}$ such that:
- $\phi_i(p_j)=\delta_{i,j}$;
- $\phi_i(p_i)=0$ on every mesh polygon not containing $p_i$.
- $\phi_i$ has an absolute max at $p_i$ and no other local max or saddle point on the polygons on which is not zero.
- Using the PDE's weak version and restricting the eq. to $\hbox{span}\,\{\phi_1,\dots,\phi_N\}\subset H^1(D)$.
Meshes
A mesh of a planar region $D$ is any collection $\{P_i\}$ of polygons s.t.:- The union $M_D$ of all $P_i$'s is an approximation of $D$, namely the measure of the set of points not in $M_D\cap D$ is small with respect to the measure of $D$.
- For any $i\neq j$, $P_i$ and $P_j$ are either disjoint or share a whole side; in particular, no vertex of one polygon falls in the interior of the side of another one.
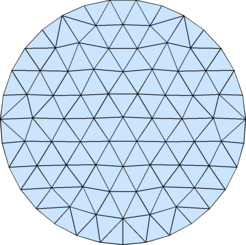
Mesh generation
Possibly the most elegant MATLAB code to generate a triangulation of the $[0,1]\times[0,1]$ square is the following by Per-Olof Persson:A great starting point for generating 2D and 3D meshes with any sort off shape is Persson's Distmesh package.m = 10; n = 10; [x,y] = ndgrid((0:m-1)/(m-1),(0:n-1)/(n-1)); pts = [x(:),y(:)]; tri = [1,2,m+2; 1,m+2,m+1]; tri = kron(tri,ones(m-1,1))+kron(ones(size(tri)),(0:m-2)'); tri = kron(tri,ones(n-1,1))+kron(ones(size(tri)),(0:n-2)'*m); trimesh(t,pts(:,1),pts(:,2),zeros(N,1))
Functions Bases
We consider just the simplest type of mesh,where all polygons in a it are triangles.
In this type of mesh, a reasonable set of $\phi_i$ is the set of piece-wise linear functions that, on any triangle $T$ of the mesh, are either identically zero or linear.
Let $(x_i,y_i)$, $i=1,2,3$ be the vertices of $T$ and $\psi_i=a_i+b_ix+c_iy$, $i=1,2,3$, the restriction to $T$ of the three basis functions that are not identically zero on $T$ and such that $\psi_i(x_j,y_j)=\delta_{ij}$.
Functions Bases
Then let $M_T= \begin{pmatrix} 1&x_1&y_1\cr 1&x_2&y_2\cr 1&x_3&y_3\cr \end{pmatrix} $. The coefficients are solutions of $ M_T \begin{pmatrix} a_1\cr b_1\cr c_1\cr \end{pmatrix} = \begin{pmatrix} 1\cr 0\cr 0\cr \end{pmatrix} , M_T \begin{pmatrix} a_2\cr b_2\cr c_2\cr \end{pmatrix} = \begin{pmatrix} 0\cr 1\cr 0\cr \end{pmatrix} , M_T \begin{pmatrix} a_3\cr b_3\cr c_3\cr \end{pmatrix} = \begin{pmatrix} 0\cr 0\cr 1\cr \end{pmatrix} \,, $namely
$$ \begin{pmatrix} a_1&a_2&a_3\cr b_1&b_2&b_3\cr c_1&c_2&c_3\cr \end{pmatrix} = M^{-1}_T $$
Implementation in MATLAB
Spectral methods
Fourier transform
Consider a $u\in C^\infty(\Bbb R)$. This is a vector space, just as $C^\infty[0,1]$ we saw earlier, but, unlike that space, it does not have a countable basis. The analogue of a bases for this space is an integral transform. Possibly the most well-known is the Fourier transform, defined as $$ \hat u(k)=\int\limits_{-\infty}^\infty u(x)\,e^{-ikx}\,dx $$ For some kind of functions, e.g. if $u\in L^2(\Bbb R)$, it is defined also the inverse Fourier transformation $$ u(x)=\frac{1}{2\pi}\int\limits_{-\infty}^\infty \hat u(k)\,e^{ikx}\,dk. $$Using Fourier Transform to solve ODEs
The main advantage of applying a Fourier transform is the following: $$ u'(x) = \frac{1}{2\pi}\int\limits_{-\infty}^\infty ik\,\hat u(k)\,e^{ikx}\,dk. $$ In other words, $d/dx$ corresponds in the momentum space to multiplication by $ik$!For example, consider $-u''(x)+u(x)=f(x)$. In momentum space the ODE just becomes the algebraic equation
$$ k^2\hat u(k)+\hat u(k)=\hat f(k) $$
so that $\hat u(k)=\hat f(k)/(1+k^2)$ and finally we get the ODE solution $$ u(x) = \frac{1}{2\pi}\int\limits_{-\infty}^\infty\frac{\hat f(k)}{1+k^2}\,e^{ikx}\,dk\,. $$
Fourier series
Consider now a bounded interval $[0,L]$. Then $C^\infty[0,L]$ has countable bases and the Fourier transform becomes a Fourier series:$$ u(x) = \sum_{k=-\infty}^\infty \hat u_k e^{2\pi ikx/L} $$
and
$$ \hat u_k = \frac{1}{L}\int\limits_{0}^L u(x) e^{-2\pi ikx/L}dx $$ so that $(u')_k = ik u_k$.
Clearly any DE under Fourier transform will become an algebraic equation, we can solve it and then use the inverse transformation to get the solution in $x$ after cutting the infinite series to $N$.
Discrete Fourier trasform
In calculations, the segment $[0,L]$ is replaced by the regular mesh $\{0,h,2h,\dots,L\}$ with $N+2$ nodes, namely $h=L/(N+1)$.Suppose we want to solve a Dirichlet problem on $[0,L]$, so that $$ u(x)=\sum_{k=1}^\infty a_k \sin(\pi kx/L) $$
Then (Discrete Fourier Tranform) $$ u_l=u(l h)=\sum_{k=1}^N a_k \sin(\pi kl/(N+1))\,,\;1\leq l\leq N $$
is a $N\times N$ system in $a_1,\dots,a_N$.
Its solution is the Inverse Discrete Fourier Tranform $$ a_k=\frac{2}{N+1}\sum_{l=1}^N u_l\sin(\pi kl/(N+1))\,. $$
Von Neumann
But how to know whether this is a "good" solution?Stability
To study the stability of the solutions of this linear system, we consider the solution $u(t,x) = e^{ik(x-c t)}$, so that $$ u_{n,j} = e^{ik(j\Delta x-c n\Delta t)} = G(k)^n e^{ikj\Delta x}\,, $$ and we plug it into the system, so that we get $$ G(k)^{n+1} e^{ikj\Delta x} = G(k)^{n} e^{ikj\Delta x} + r\left(G(k)^{n} e^{ik(j+1)\Delta x}-G(k)^{n} e^{ik(j-1)\Delta x}\right)\,, $$ namely $ G(k) = 1 - i\frac{r}{2} \sin\left(k\Delta x\right)\,. $Hence $|G(z)|>1$ for any value of $r$, namely this numerical method is unstable for any choice of $\Delta t$ and $\Delta x$!
A remedy: the Lax–Friedrichs method
We can fix this problem by replacing the term $u_{n,j}$ in the expression of $u_t$ with the space average$$ \frac{u_{n,j+1}+u_{n,j-1}}{2}\,, $$
so that the system becomes
$$ u_{n+1,j} = \frac{u_{n,j+1}+u_{n,j-1}}{2} + \frac{r}{2}\left(u_{n,j+1}-u_{n,j-1}\right)\,, $$
Under the guess $u(t,x) = e^{ik(x-ct)}$ we find that
$$ G(k) = \cos\left({k\Delta x}\right) + i\,r\cos\left({k\Delta x}\right) $$
so that $|G(k)|\leq1$ when $c\Delta t\leq\Delta x$.