Press ? for presentation controls.
Best viewed in Firefox,
Chrome and
Opera.
Backward dynamics
in
S-unimodal maps
Joint work with Jim Yorke
Howard University
Washington, DC (USA)
Motivations
Qualitative Behavior
A fundamental goal of Dynamical Systems theory:
of all possible forward/backward trajectories
under a given (discrete or continuous) flow.
In this talk I will illustrate the qualitative
forward and backward behavior of S-unimodal maps.
I will use the logistic map family as my source of examples.
Finally, I will encode the information about the qualitative dynamics
in a graph, as Ana nicely illustrated in the previous talk.
A few Definitions
Bitrajectories
A discrete dynamical system on a topological space$x_0=x$ ;$x_{i+1}=f(x_i)$ for all$i\in\Bbb Z$ .

$s\alpha$ and $\omega$ limits
Given a bitrajectory
we denote by
and by
Given a point
its
Chain-recurrent points
For each bitraj.|
A point $x$ is an $\varepsilon$-chain from $x$ to itself. We denote by |

|
Attracting and repelling Nodes
A main feature ofnamely a closed invariant set $A\subset M$ such that
Graph
of the
logistic map
The logistic map
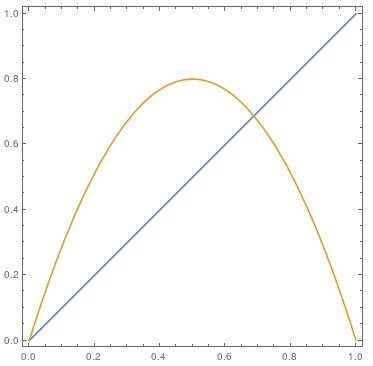
|
|
Bifurcation diagram of the logistic map

| Nodes coloring: | |
| Black: | Attractor |
| White: | Fixed endpoint |
| Periodic orbits | |
| Cantor sets | |
The period-3 window of the logistic map

| Nodes coloring: | |
| Black: | Attractor |
| White: | Fixed endpoint |
| Periodic orbits | |
| Cantor sets | |
Backward Limits
Backward dense orbits within nodes
Type of nodes in S-unimodal maps:
Repelling : periodic orbits,subshifts of finite type .Attracting : periodic orbits,adding machines ,cycles of intervals .
Backward dense orbits within nodes
Type of nodes in S-unimodal maps:
Repelling : periodic orbits,subshifts of finite type .Attracting : periodic orbits,adding machines ,cycles of intervals .
2. every irreducible 2-sided shift has a doubly transitive point.
Backward dense orbits within nodes
Type of nodes in S-unimodal maps:
Repelling : periodic orbits,subshifts of finite type .Attracting : periodic orbits,adding machines ,cycles of intervals .
Then each $x\in S$ has a backward dense trajectory.
Backward dense orbits within nodes
Type of nodes in S-unimodal maps:
Repelling : periodic orbits,subshifts of finite type .Attracting : periodic orbits,adding machines ,cycles of intervals .
Then each $x\in A$ has a backward dense trajectory.
Backward dense orbits within nodes
Type of nodes in S-unimodal maps:
Repelling : periodic orbits,subshifts of finite type .Attracting : periodic orbits,adding machines ,cycles of intervals .
Let $x$ belong to a node $N$ of a S-unimodal map $f$.
Then $N\subset s\alpha_f(x)$.
General s$\alpha$ limits
I will illustrate general s$\alpha$ limits in a few examples.
The graph of the logistic map clearly shows that
Roughly speaking,
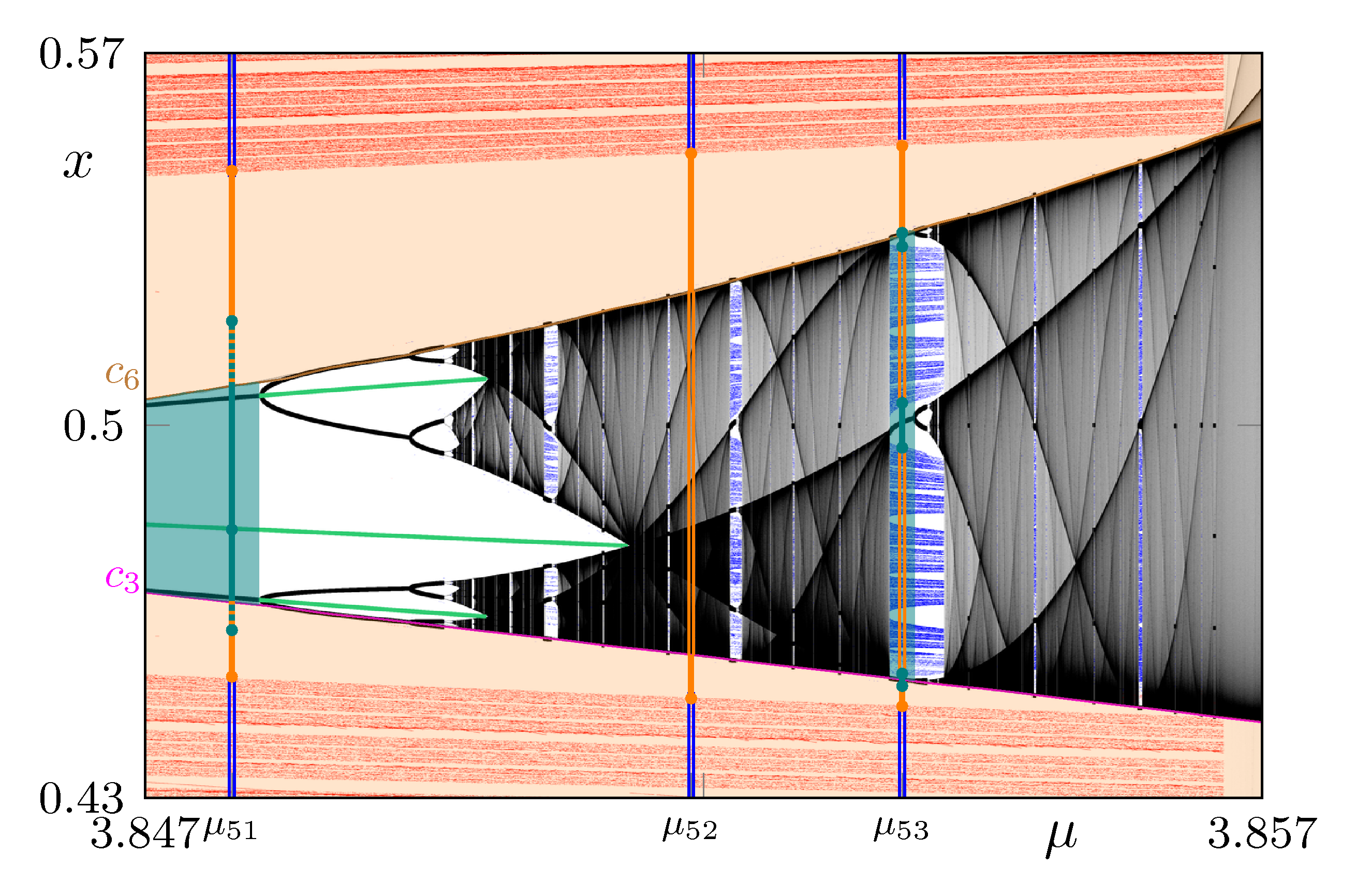
Example 1
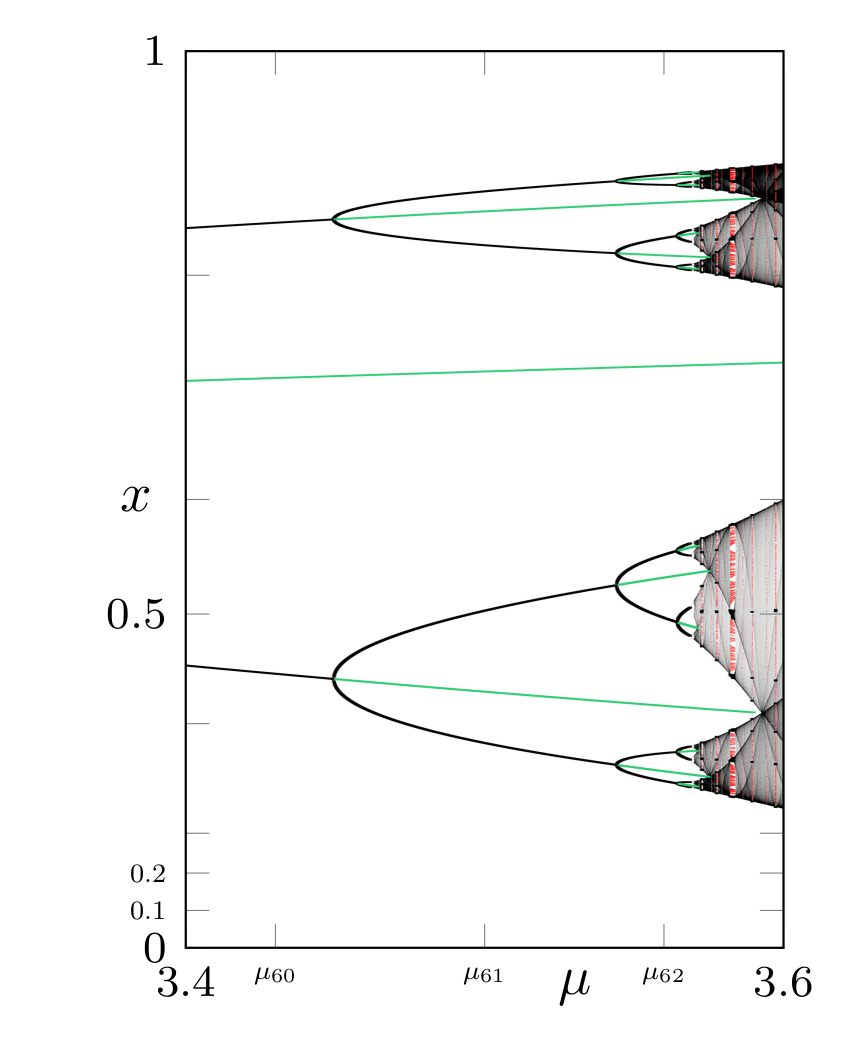
Example 1
$c_k = \ell_\mu^k(c_0)$
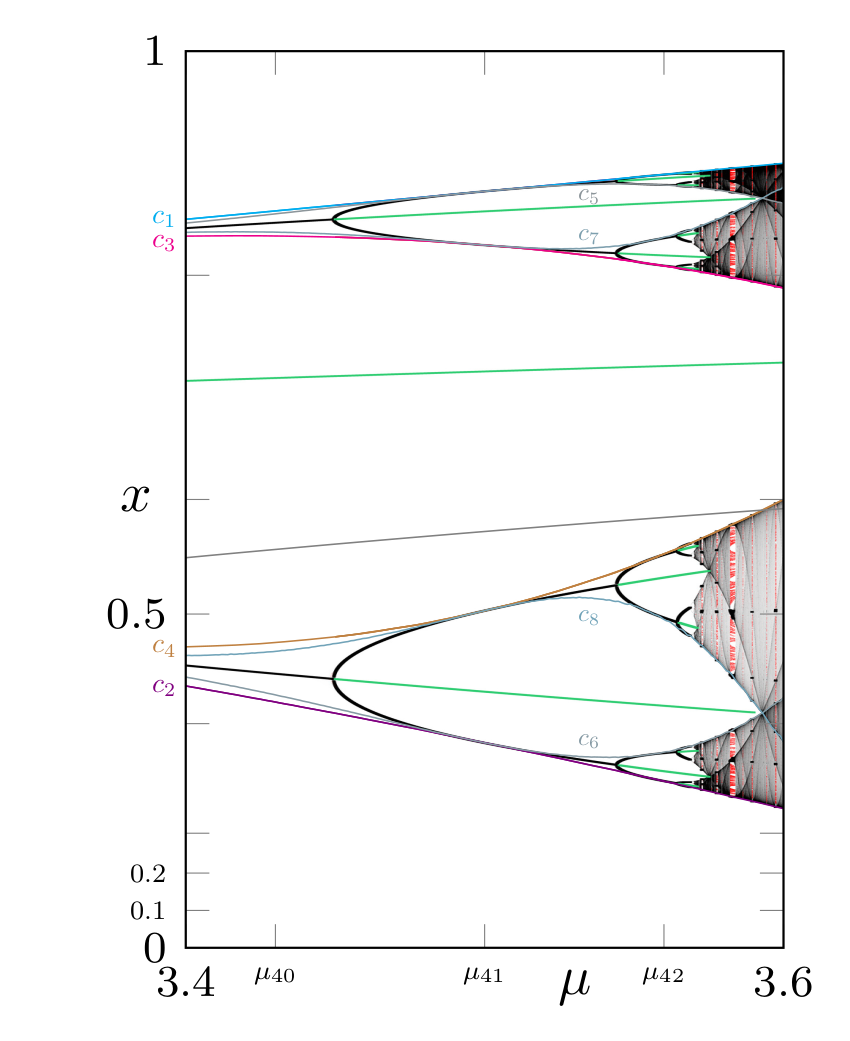
Example 1
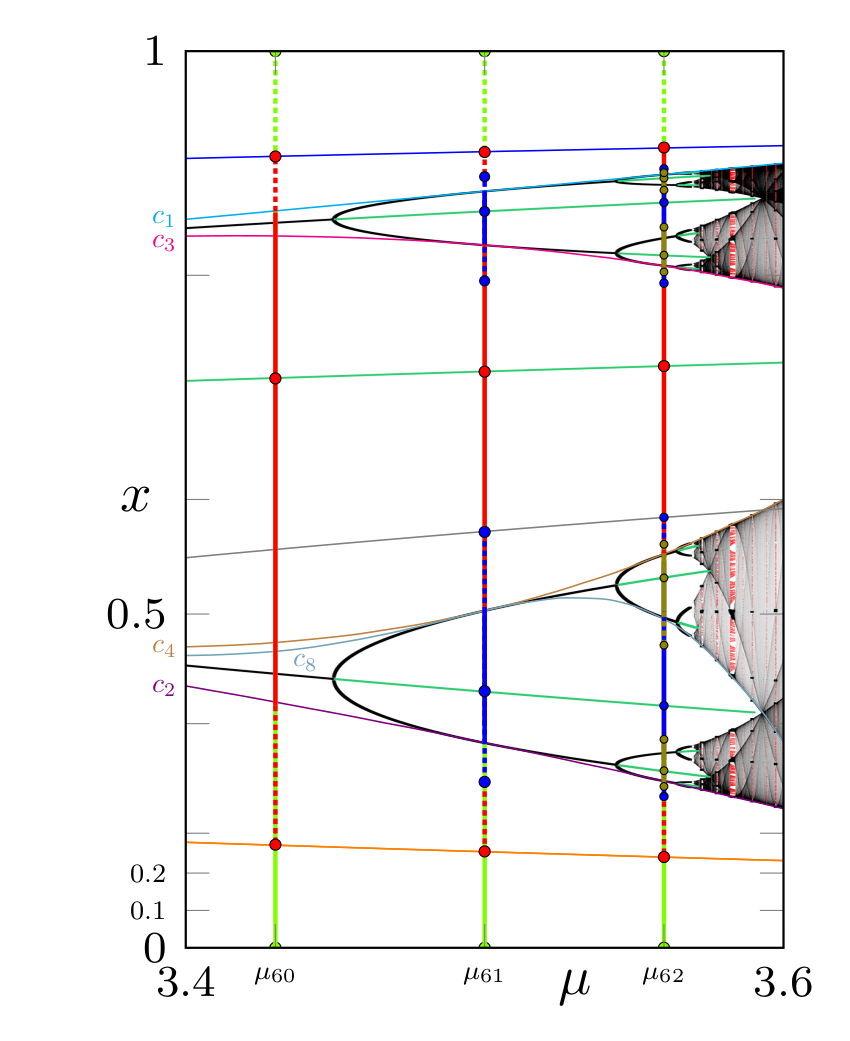
Example 1

Example 2

Example 2

Example 3
What's next

What's next
Graph and backward dynamics of multimodal maps
jointly with Ana Anusic.General properties of graphs of dynamical systems
jointly with Jim Yorke.Graphs of reaction-diffusion parabolic PDEs
jointly with Jim Yorke.
Discrete & Continuous Dynamical Systems, 41:11 (2021) Jim Yorke, RdL, Infinite towers in the graphs of many dynamical systems,
Nonlinear Dynamics, 105 (2021) RdL, Backward asymptotics in S-unimodal maps, IJBC, 32:6 (2022) Ana Anusic, RdL, Graph and backward asymptotics of the tent map Jim Yorke, RdL, Graphs of dynamical systems, in preparation