Dynamical Systems -- Theory and Applications, 6 December 2021

Press ? for presentation controls.
Best viewed in Firefox, Chrome and Opera.

Infinite towers
in the graph
of a Dynamical System

Roberto De Leo

roberto.deleo@howard.edu

Howard University
Washington, DC (USA)

Joint work with Jim Yorke

The logistic map

$\ell_\mu(x)=\mu x(1-x)$,

$x\in[0,1]$,  $\mu\in(1,4)$

  1. $\ell_\mu$ has a unique attractor $A_\mu$ and almost all points asymptote to it;

  2. the fixed point $x=0$
    is repelling;

  3. $\ell_\mu$ is not surjective.

  4. Hence, $\ell_\mu$ has at least two nodes (the fixed point 0 and the attractor).

    (By nodes here we mean invariant sets with a dense orbit. We call them nodes because they can be seen as the nodes of a graph.)

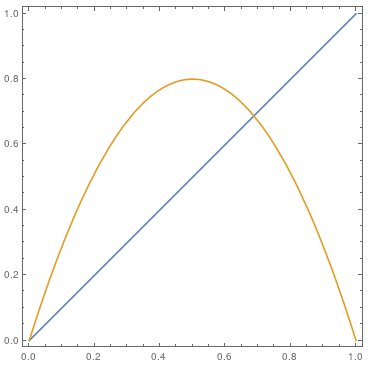
Bifurcation diagram of the logistic map

Types of attracting nodes:
  1. Periodic orbit
  2. Feigenbaum attractor
  3. Cycle of intervals (chaotic)
  4. Beginning of a window
  5. End of a window
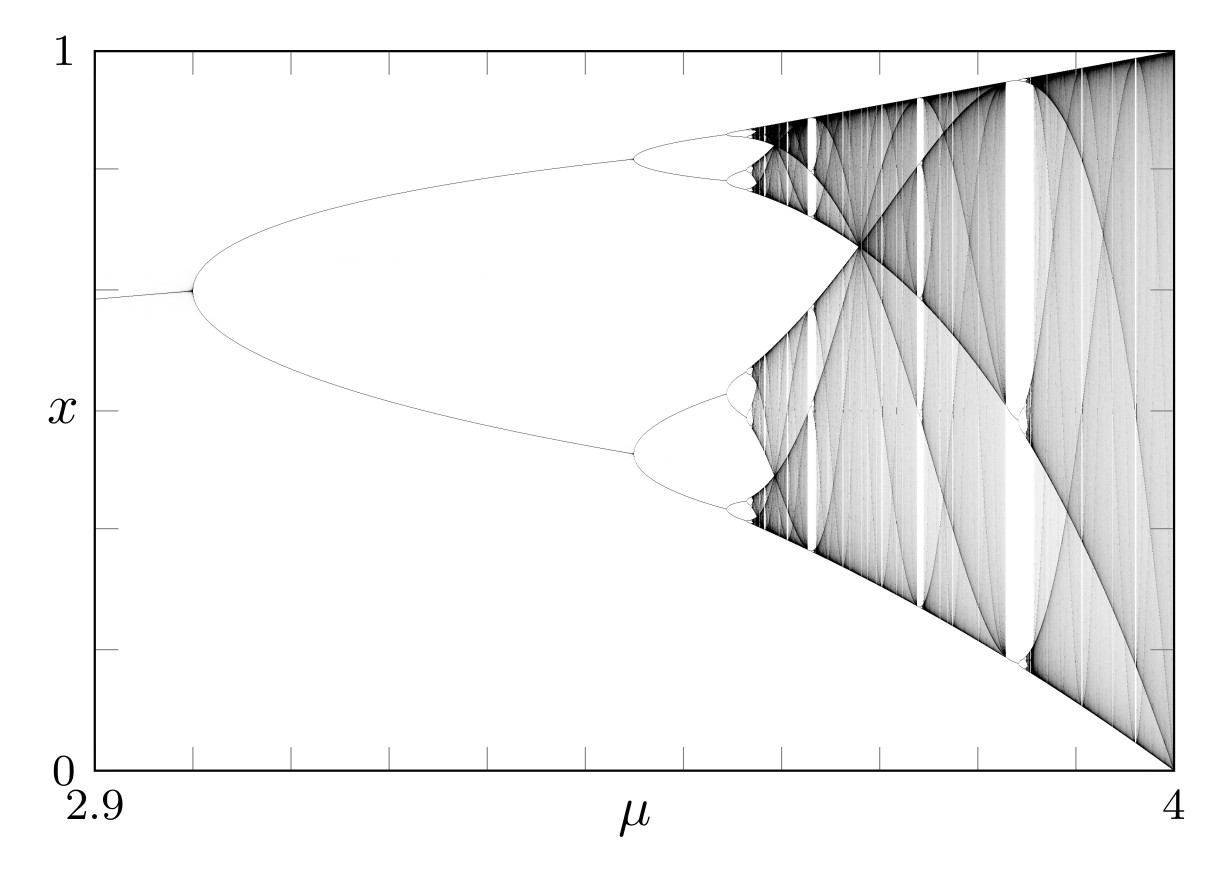
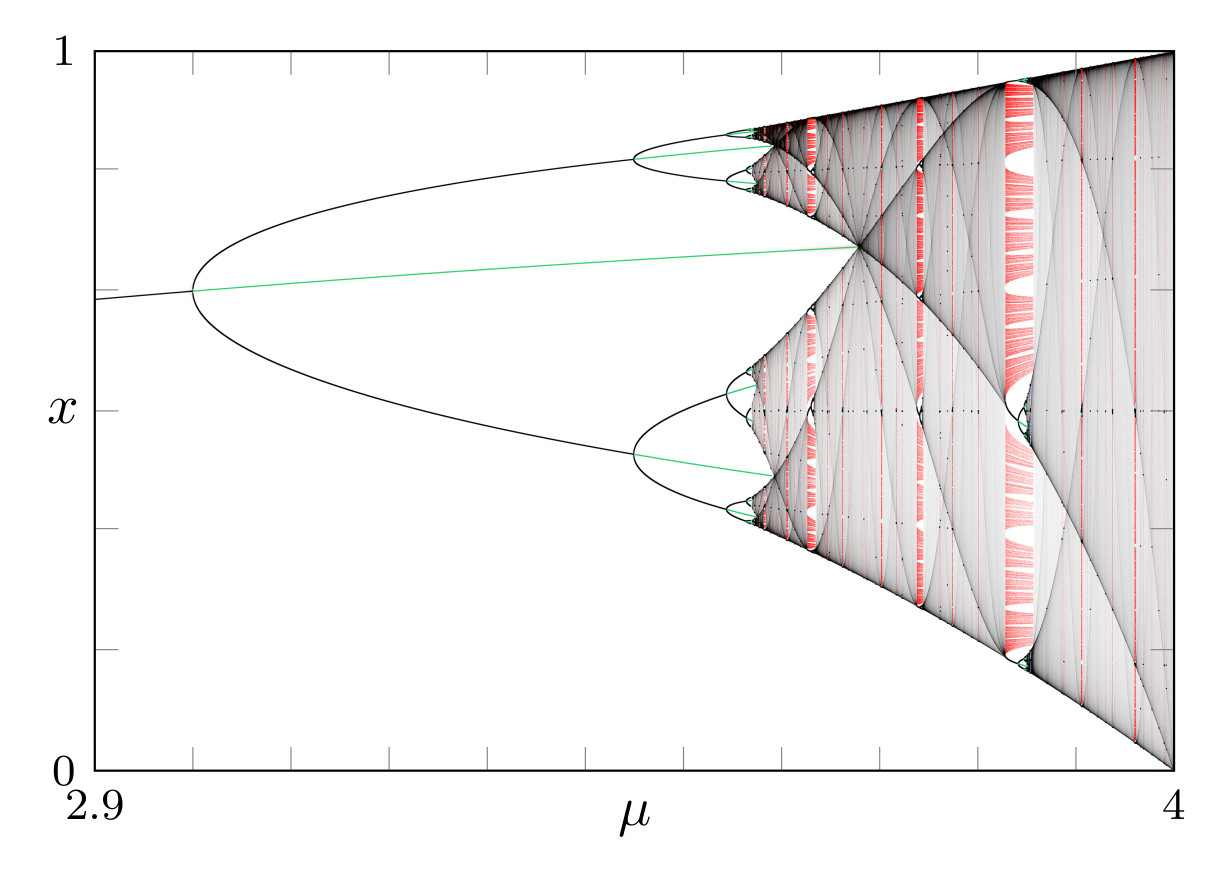
This picture shows the attracting nodes for each $\mu$.

Bifurcation diagram of the logistic map

Types of repelling nodes:
  1. Periodic orbit
  2. Cantor set
    (subshift of finite type)
This picture shows all (visible) nodes for each $\mu$.

L. Jonker
D. Rand
S. van Strien
J. Guckenheimer
M. Lyubich
A. Blokh

+

C. Conley

The period-3 window of the logistic map

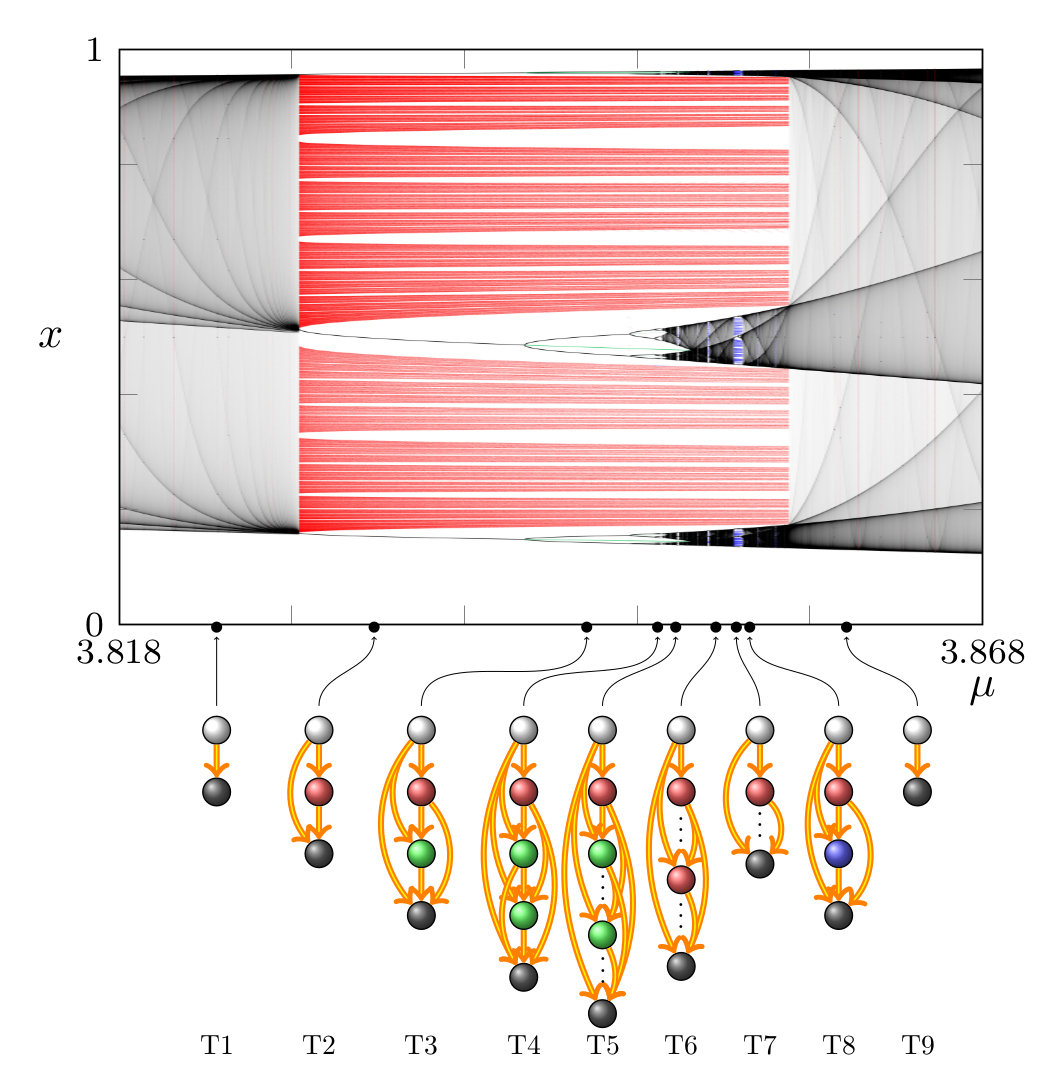
Theorem [Conley '76, Norton '95]
Each discrete dynamical system $f:X\to X$ on a compact metric space $X$ has a Lyapunov function.

In particular, for each $x\in X$, either
1. $x$ lies on a node of $f$;
or
2. $x$ lies on a bi-infinite trajectory whose backward limit lies in some node $M$ and its forward limit on some other node $N\neq M$.

Theorem [J. Yorke & RdL, 2021]
The graph of the logistic map
is a tower,

namely there is an edge
between each pair of nodes.

The Lorenz system

$$ \left\{ \begin{array}{@{}l@{}} \dot x&=-\sigma x+\sigma y\cr \dot y&=-xz+rx-y\cr \dot z&=\phantom{-}xy-bz\cr \end{array} \right. $$

For $r>1$, the Lorenz system has three fixed points:
the origin and the points $$ C_\pm=(\pm\sqrt{b(r-1)},\pm\sqrt{b(r-1)},r-1). $$

On the plane $z=r-1$, solutions passing close to $C_\pm$ will return and cut again the plane nearby $C_\pm$ and so on, so we can define on that plane a Poincaré map.

Bifurcation diagram of the Lorenz system

Projection on the $(y,r)$ plane of the attracting nodes

A period-3 window of the Lorenz system

References

Jim Yorke, RdL, "The graph of the logistic map is a tower",
Discrete & Continuous Dynamical Systems, 41:11 (2021)

Jim Yorke, RdL, "Infinite towers in the graphs of many dynamical systems",
Nonlinear Dynamics, 105 (2021)

RdL, "Backward asymptotics in S-unimodal maps", arXiv

Thank you!!

Then:

If $k=p$ If $k < p$
  1. if $x\in N_p$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_p\;$;

  2. otherwise,

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_{r}$
    where $r=p-1$ or $r=p-2$.
  1. if $x\in N_k$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_k\;$;

  2. otherwise,


    where $r$ can be either $k$ or $k-1$ or $k-2$.