23rd European Conference on Iteration Theory, 16 June 2022

Press ? for presentation controls.
Best viewed in Firefox, Chrome and Opera.

Backward dynamics
in S-unimodal maps

Roberto De Leo
<roberto.deleo@howard.edu>

Howard University
Washington, DC (USA)

Joint work with Jim Yorke

Motivations

Inverse Limits

Given a map $p:M\to M$, $\alpha_p(x)$ is the set of all $y\in M$ s.t.
arbitrarily close to $y$ there are points falling on $x$ under $p$.

Theorem [Fatou 1920] Let $r$ be a rational complex map of deg $>1$. Then $\alpha_r(z)$ equals the Julia set of $r$ for almost all $z\in\Bbb C$.

Numerically one gets similar results in case of real Newton maps

(see below Newton's map of $p(x,y)=(x(x^2-1)+60y,y(y^2-1)-x)$),

but in this case Fatou's theorem
only holds for some non-empty, non-dense open set.

Main Question

What can be said in general
about the inverse dynamics
in a discrete dynamical system?

The answer is strictly related to the
qualitative dynamics nearby invariant sets.

In the remainder of the talk
I will answer this question referring to the the logistic map
but all my arguments hold for any S-unimodal map.

The answer will be encoded in a graph describing the qualitative behavior of the corresponding dyamics.

A few Definitions

Def 1: Trajectories of a discrete DS

A discrete dynamical system on a topological space $M$

is a continuous map $f:M\to M$.

 

A bitrajectory based at $x\in M$ is a bi-infinite sequence

$\dots x_{-2},x_{-1},x_0,x_1,x_2\dots$

such that:

  1. $x_0=x$;
  2. $x_{i+1}=f(x_i)$  for all  $i\in\Bbb Z$.

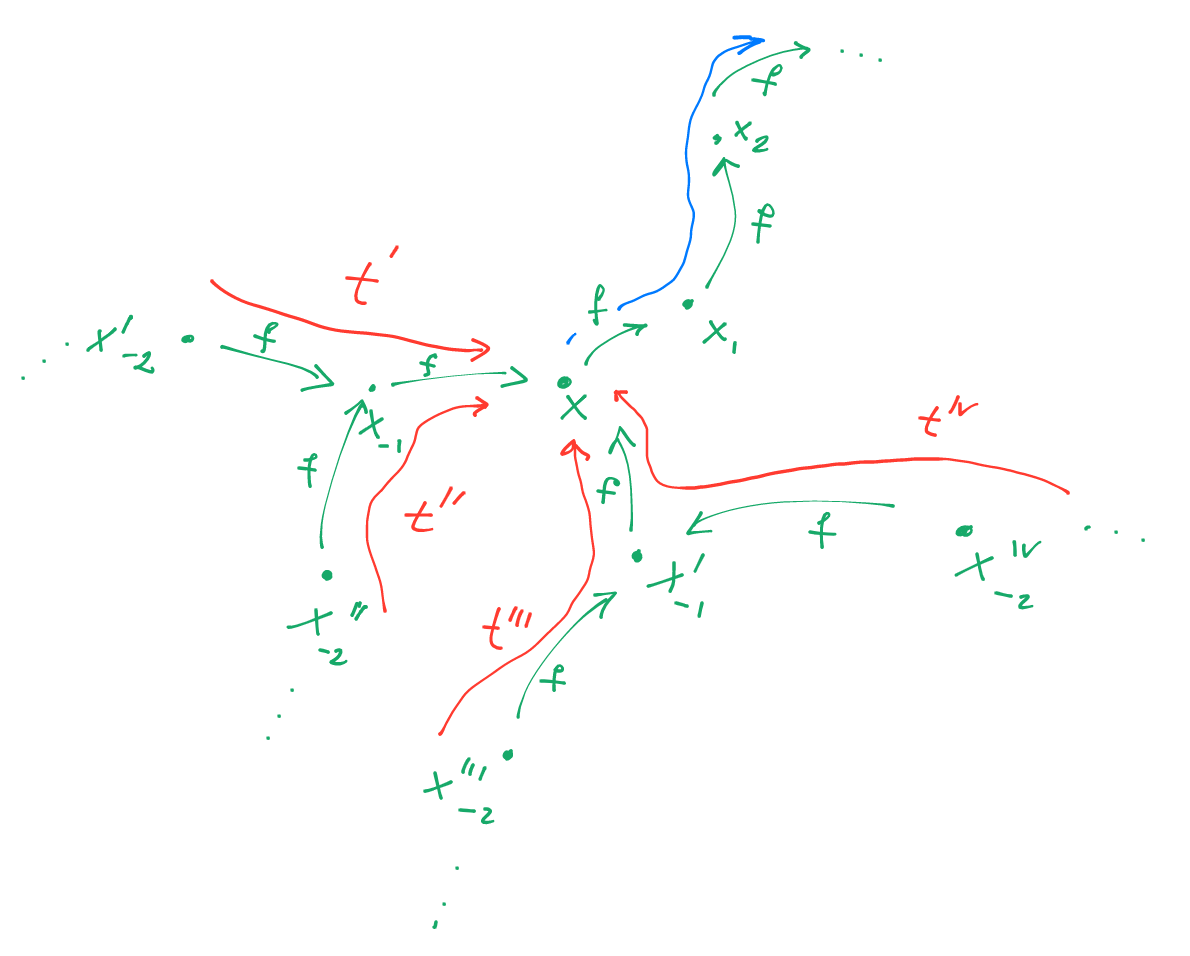
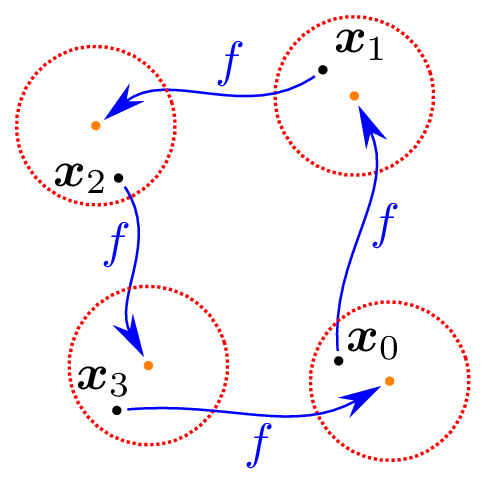
Def 2: $s\alpha$ and $\omega$ limits

Given a bitrajectory $t=\{\dots,x_{-2},x_{-1},x_0,x_1,x_2,\dots\}$,

we denote by $\omega(t)$ the set of the limit points of $t$ for $i\to+\infty$

and by $\alpha(t)$ the set of the limit points of $t$ for $i\to-\infty$.

Given a point $x\in M$,
its $\omega$-limit is the set of the limit points of its forward trajectory.

Its $s\alpha$-limit (M. Hero, 1992), in turn, is the set

$s\alpha_f(x)=\cup_{t_x}\alpha(t_x)$,

where the union is over all bitrajectories $t_x$ based at $x$.

Def 3: Chain-recurrent points

For each bitraj. $t$, all points of $\omega(t)$ and $\alpha(t)$ are chain-recurrent.

An $\varepsilon$-chain is a sequence $x_0,x_1,x_2,\dots$ such that

$d( f(x_i), x_{i+1} ) < \varepsilon$

for all $i=0,1,2,\dots$

A point $x$ is chain-recurrent if, for every $\varepsilon > 0$, there is
an $\varepsilon$-chain from $x$ to itself.

We denote by ${\cal R}_f\subset M$ the set of all chain-recurrent pts of $f$.

Def 4: Attracting and repelling Nodes

A main feature of chain-recurrence is the following:

within the set $\cal R_f$ of all chain-recurrent points, the relation

$x\sim y$ if for all $\varepsilon>0$ there are $\varepsilon$-chains from $x$ to $y$ and from $y$ to $x$

is an equivalence relation.

We call nodes the equivalence classes of $\cal R_f$.

From now on we assume that $M$ is also a measure space and we say that a node $N$ $\subset\cal R_f$ is attracting if it contains an attractor,
namely a closed invariant set $A\subset M$ such that

$\omega_f(x)\subset A$ for a set of points $x\in M$ of positive measure.

If $N$ is not attracting, we say that $N$ is repelling.

Graph
of the
logistic map

The logistic map

$\ell_\mu(x)=\mu x(1-x)$,

$x\in[0,1]$,  $\mu\in(1,4)$

  1. $\ell_\mu([0,1])\subset [0,1]$;

  2. $\ell_\mu$ has a unique attractor $A_\mu$ and almost all points asymptote to it;

  3. the fixed point $x=0$ is repelling;

  4. $\ell_\mu$ is not surjective.

  5. Hence, $\ell_\mu$ has at least two nodes
    (the fixed point 0 and the attractor).

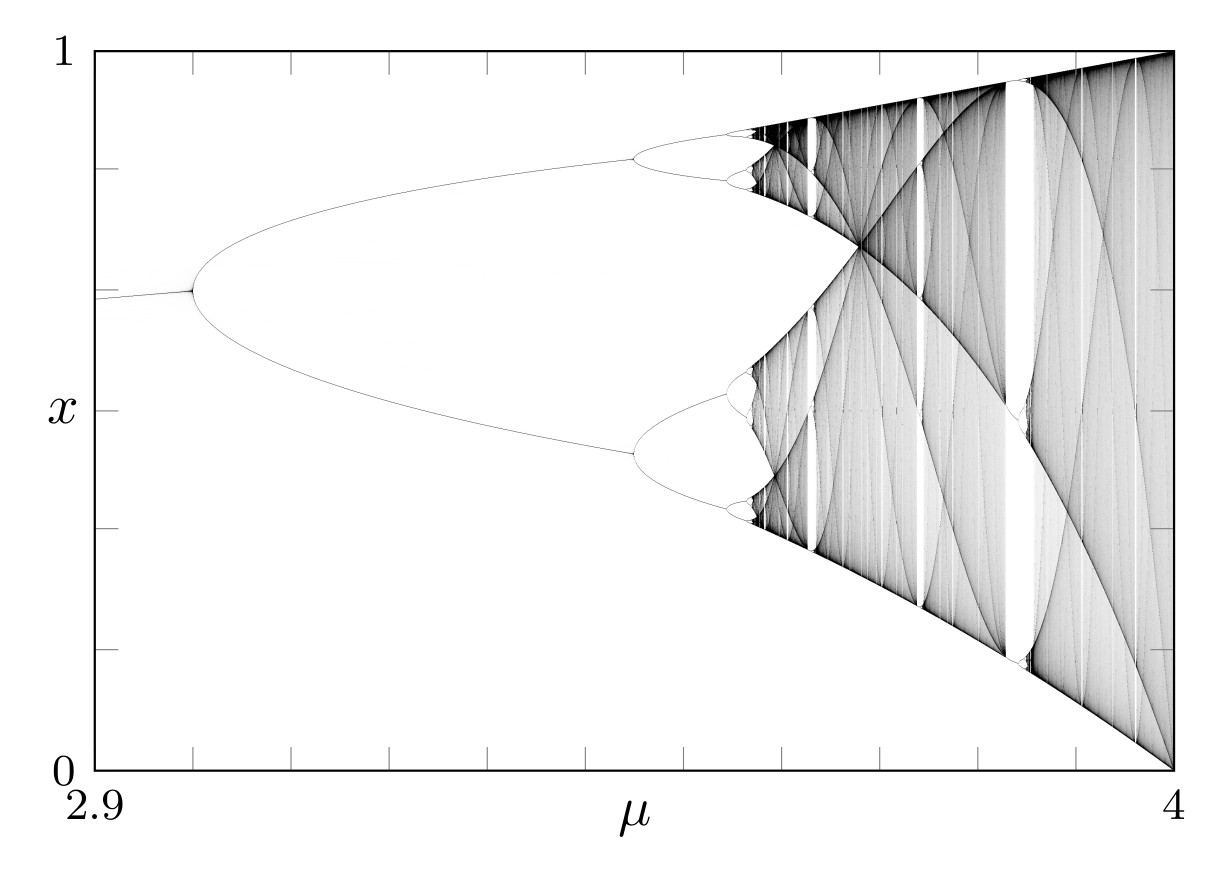
Bifurcation diagram of the logistic map

Prop [Yorke & RdL]
There are 5 types of attracting nodes:
  1. Periodic orbit
  2. Feigenbaum attractor
  3. Cycle of intervals (chaotic)
  4. Beginning of a window
  5. End of a window
This picture shows the attracting nodes for each $\mu$.

L. Jonker
D. Rand
S. van Strien
J. Guckenheimer
M. Lyubich
A. Blokh

+

C. Conley

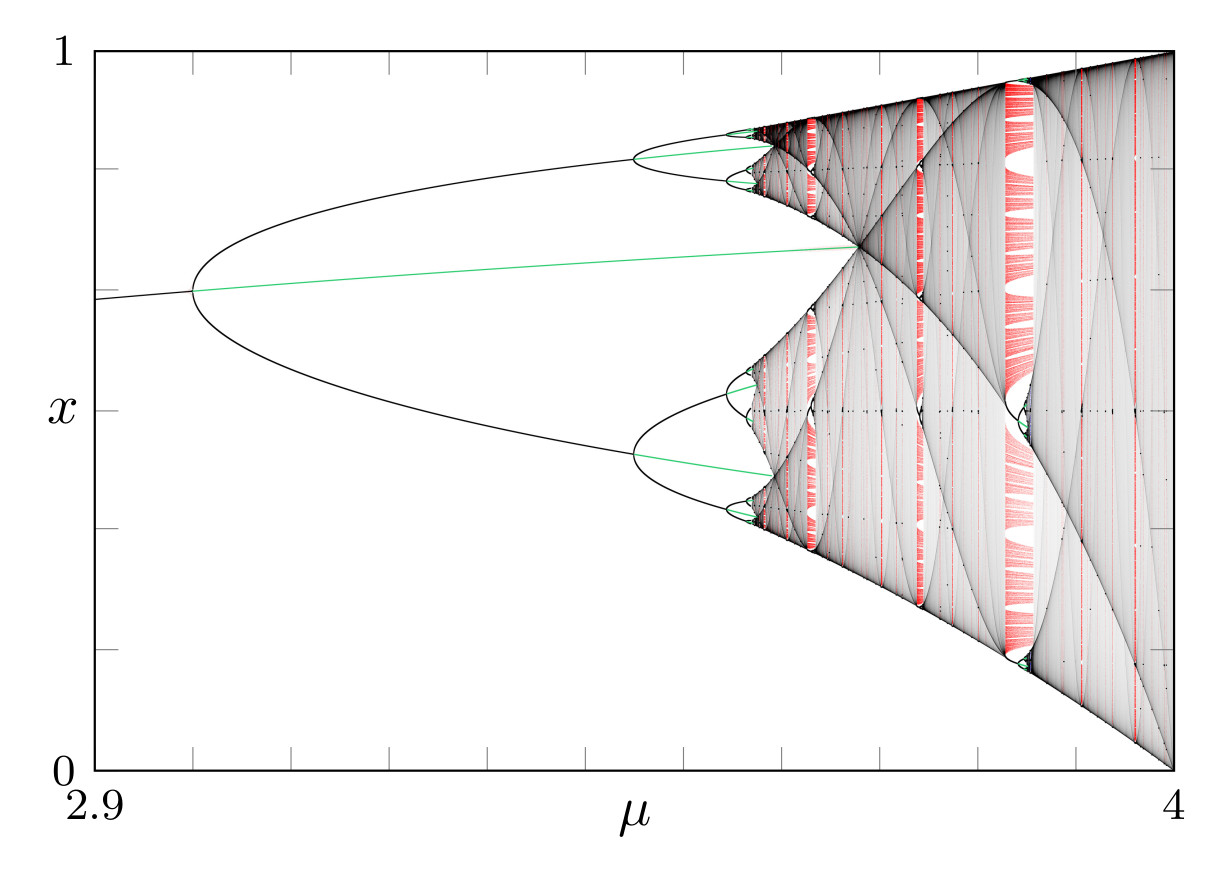
Bifurcation diagram of the logistic map

Prop [Yorke & RdL]
There are 2 types of repelling nodes:
  1. Periodic orbit
  2. Cantor set
    (subshift of finite type)
This picture shows all (visible) nodes for each $\mu$.

L. Jonker
D. Rand
S. van Strien
J. Guckenheimer
M. Lyubich
A. Blokh

+

C. Conley

The period-3 window of the logistic map

Theorem [Conley '76, Norton '95]
Each discrete dynamical system $f:X\to X$ on a compact metric space $X$ has a Lyapunov function.

In particular, for each $x\in X$, either
1. $x$ lies on a node of $f$;
or
2. $x$ lies on a bi-infinite trajectory whose $\alpha$-limit lies in some node $M$ and its $\omega$-limit on some other node $N\neq M$.

So we can associate a graph $\Gamma_f$ to any DS $f:M\to M$.

1. The nodes of $\Gamma_f$ are the equivalence classes of $\cal R_f$.

2. There is an edge
from node $M$ to node $N$
if there is a bitrajectory $t$ s.t. $\omega_f(t)\subset N$ and $\alpha_f(t)\subset M$.

Note that $\Gamma_f$ cannot have loops.

The period-3 window of the logistic map

Theorem [Yorke & RdL, 2021]
The graph of the logistic map is a tower,

namely there is an edge
between each pair of nodes.

Since $\Gamma_f$ has no loops, this means that nodes can be sorted linearly: $N_0,N_1,\dots,N_{p-1},N_p$.

Arbitrarily close to $N_i$,
for each $j\geq i$ there are points asymptoting to $N_j$.

No point close enough to $N_i$
can asymptote to $N_j$ for $j>i$.

Inverse Limits

The graph of the logistic map clearly shows that
there is a natural hierarchy among nodes.
This same hierarchy is reflected in the backward limits.

 

Roughly speaking,
the closer a point is to the attractor, the larger is its $s\alpha$-limit set.
The extreme cases are:

1. The $s\alpha$-limit set of any point close enough to 1 is empty;

2. The $s\alpha$-limit set of any point close enough to 0 contains only 0;

3. The $s\alpha$-limit set of any point in the attractor
is the whole non-wandering set $\Omega_{\ell_\mu}$
(note that, for almost all $\mu$, $\;\Omega_{\ell_\mu}$ coincides with $\cal R_{\ell_\mu}$).

Example 1

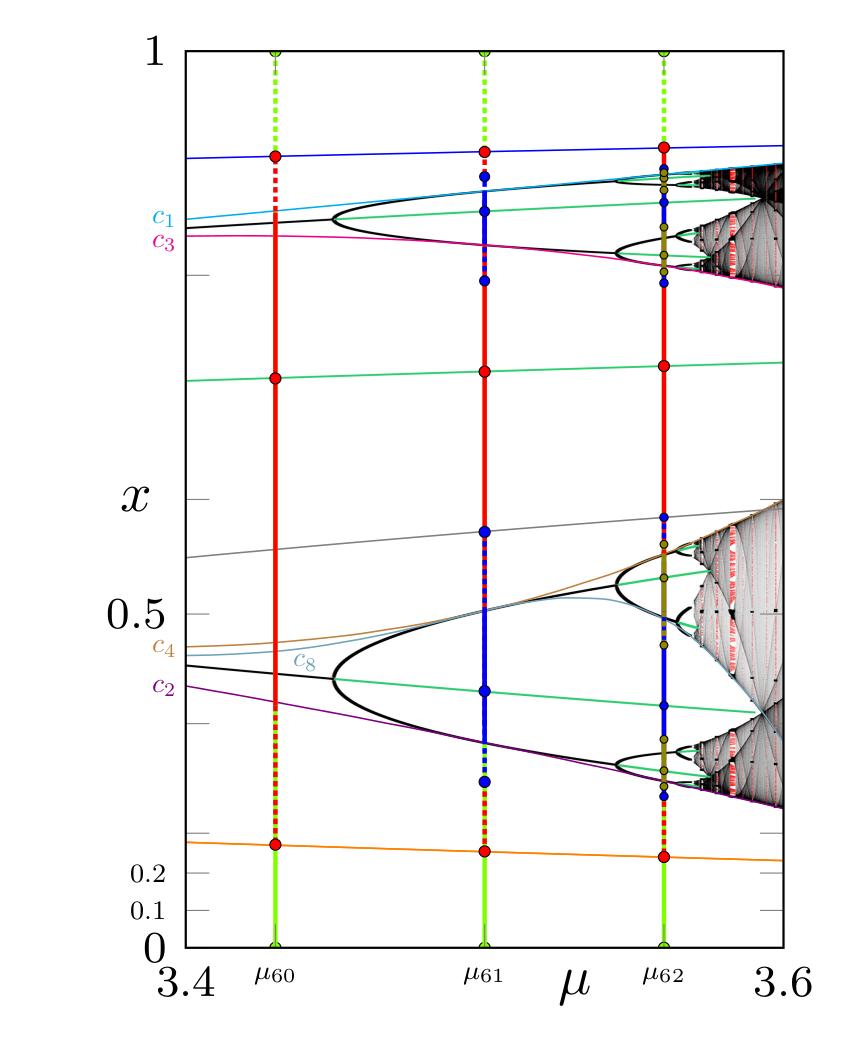
Example 1

Example 2

Example 2

Example 3

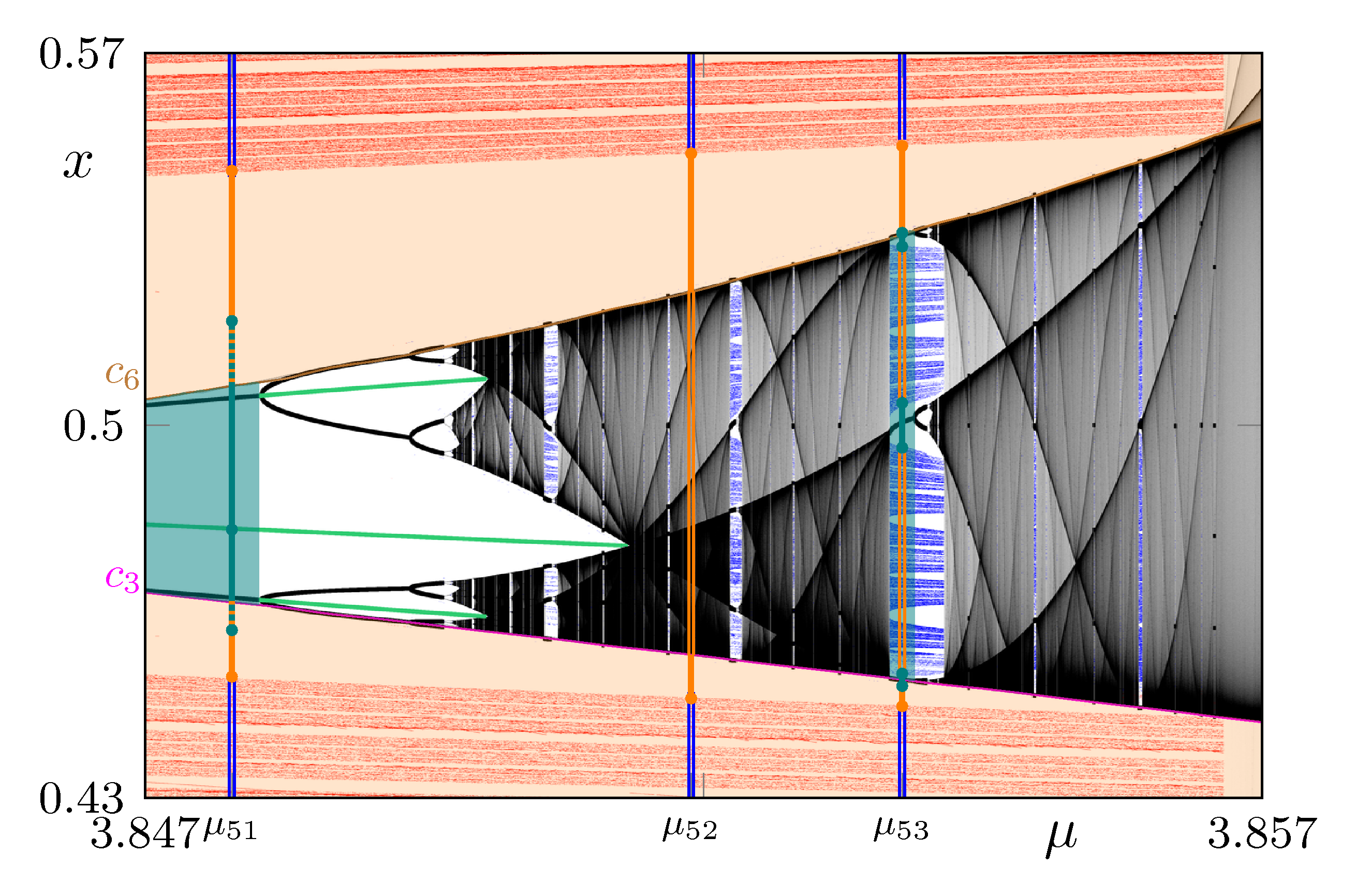
RdL, Conjectures about simple dynamics for real Newton maps on ${\Bbb R}^2$,
Fractals, 27:6, 2019.

RdL, Julia sets of Newton maps of real quadratic polynomial maps on the plane, IJBC, 30:9 (2020).

Jim Yorke, RdL, The graph of the logistic map is a tower,
Discrete & Continuous Dynamical Systems, 41:11 (2021)

Jim Yorke, RdL, Infinite towers in the graphs of many dynamical systems,
Nonlinear Dynamics, 105 (2021)

RdL, Backward asymptotics in S-unimodal maps, IJBC, 32:6 (2022)

 
Thank you!!

Then:

If $k=p$ If $k < p$
  1. if $x\in N_p$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_p\;$;

  2. otherwise,

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_{r}$
    where $r=p-1$ or $r=p-2$.
  1. if $x\in N_k$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_k\;$;

  2. otherwise,


    where $r$ can be either $k$ or $k-1$ or $k-2$.