James Yorke's 80th Birthday Celebration, 18 September 2021

Press ? for presentation controls.
Best viewed in Firefox, Chrome and Opera.

Dynamics of
the Logistic map

Joint work with Jim Yorke

Roberto De Leo

roberto.deleo@howard.edu

Howard University
Washington, DC (USA)

The logistic map

$\ell_\mu(x)=\mu x(1-x)$,

$x\in[0,1]$,  $\mu\in(1,4)$

  1. $\ell_\mu$ has a unique attractor $A_\mu$ and almost all points asymptote to it;

  2. the fixed point $x=0$ is repelling;

  3. $\ell_\mu$ is not surjective.

  4. Hence, $\ell_\mu$ has at least two nodes
    (the fixed point 0 and the attractor).

    (By nodes here we mean invariant sets with a dense orbit. We call them nodes because they can be seen as the nodes of a graph.)

Bifurcation diagram of the logistic map

Types of attracting nodes:
  1. Periodic orbit
  2. Feigenbaum attractor
  3. Cycle of intervals (chaotic)
  4. Beginning of a window
  5. End of a window
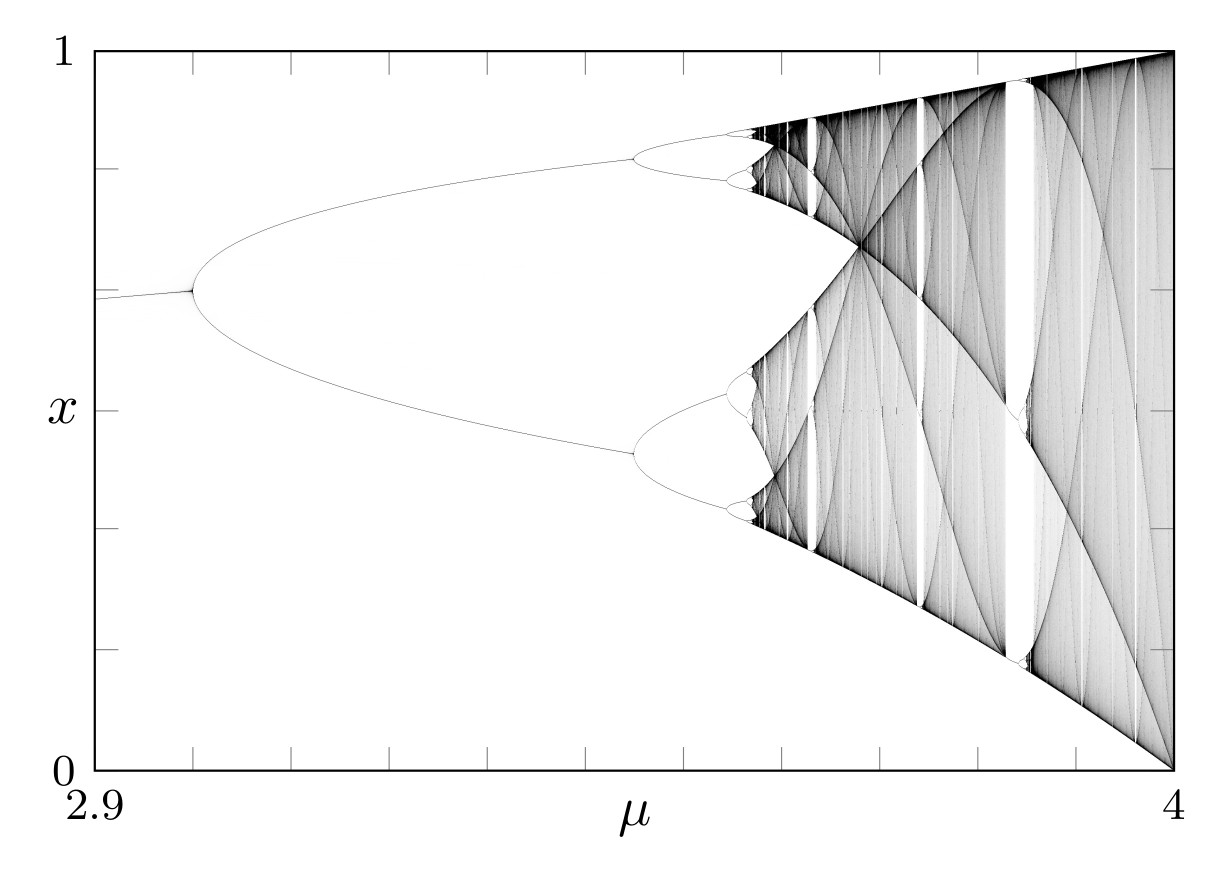
This picture shows the attracting nodes for each $\mu$.

Bifurcation diagram of the logistic map

Types of repelling nodes:
  1. Periodic orbit
  2. Cantor set
    (subshift of finite type)
This picture shows all (visible) nodes for each $\mu$.

L. Jonker
D. Rand
S. van Strien
J. Guckenheimer
M. Lyubich
A. Blokh

+

C. Conley

The period-3 window of the logistic map

Theorem [Conley '76, Norton '95]
Each discrete dynamical system $f:X\to X$ on a compact metric space $X$ has a Lyapunov function.

In particular, for each $x\in X$, either
1. $x$ lies on a node of $f$;
or
2. $x$ lies on a bi-infinite trajectory whose backward limit lies in some node $M$ and its forward limit on some other node $N\neq M$.

Theorem [J. Yorke & RdL, 2021]
The graph of the logistic map is a tower,

namely there is an edge
between each pair of nodes.

Projection of the bifurcation diagram
of the Poincaré map of the Lorenz system

A window of the Poincaré map
of the Lorenz system

Backward asymptotics in the Logistic map

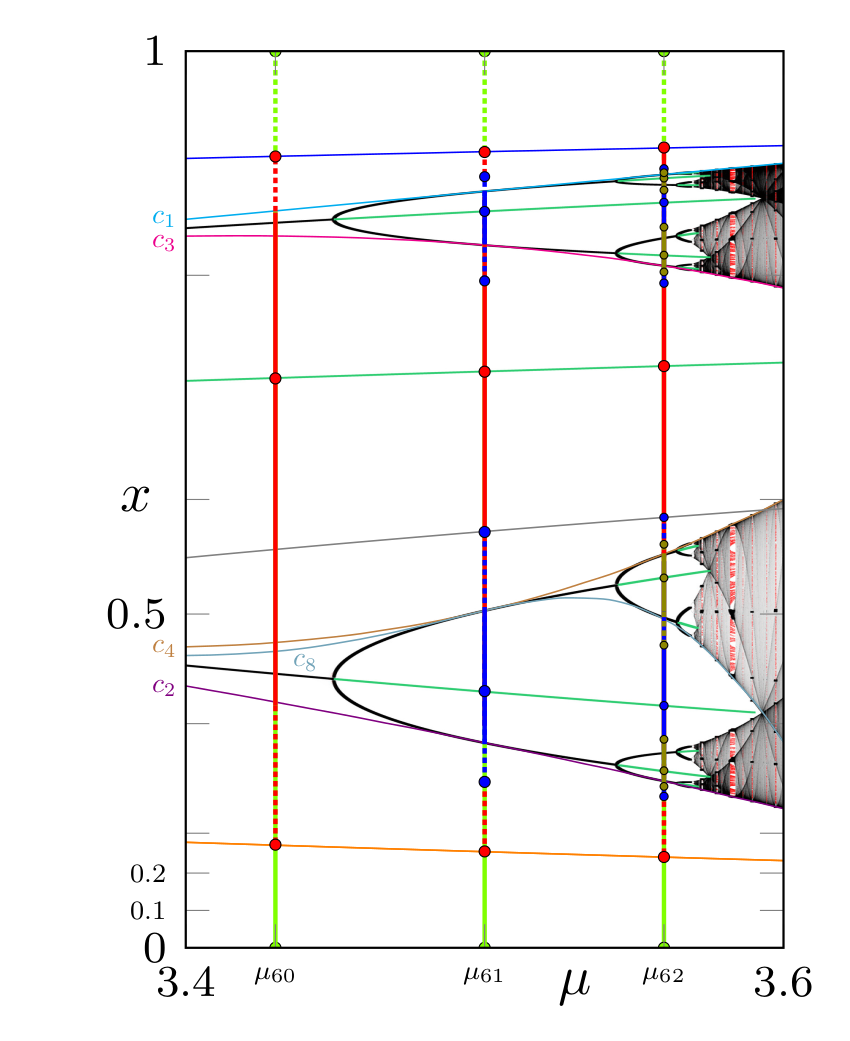
Backward asymptotics in the Logistic map

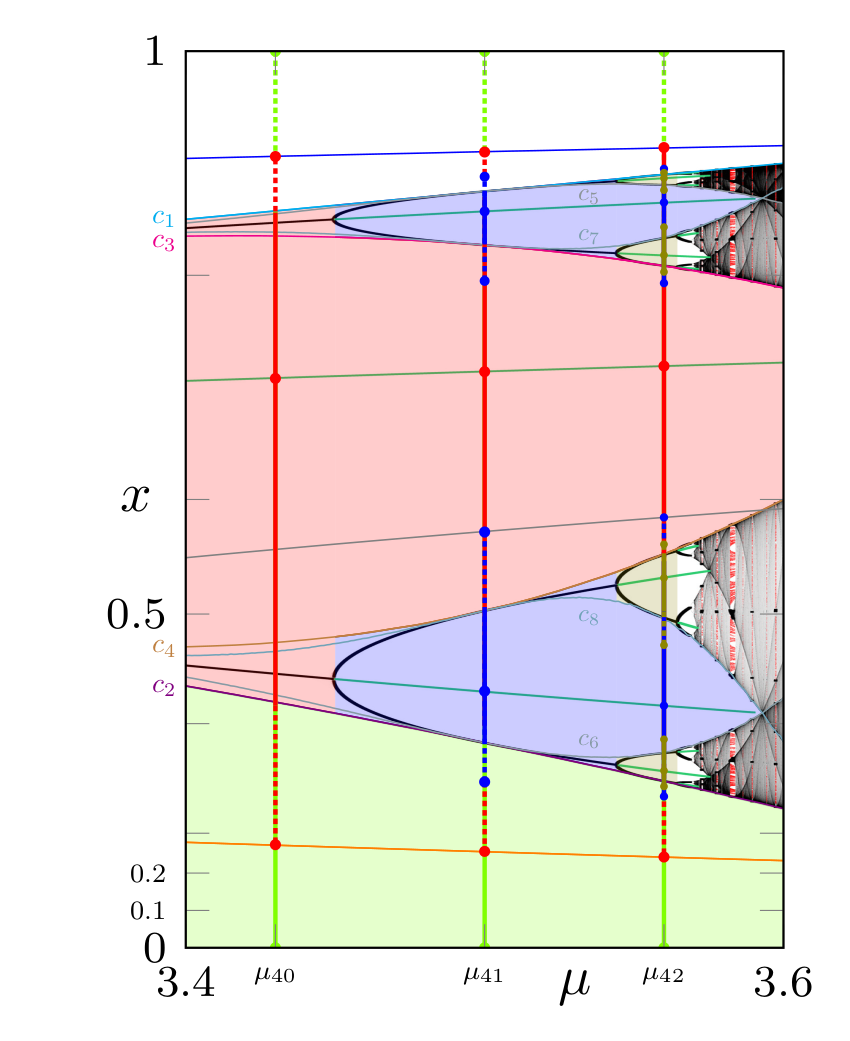
Backward asymptotics in the Logistic map

Backward asymptotics in the Logistic map

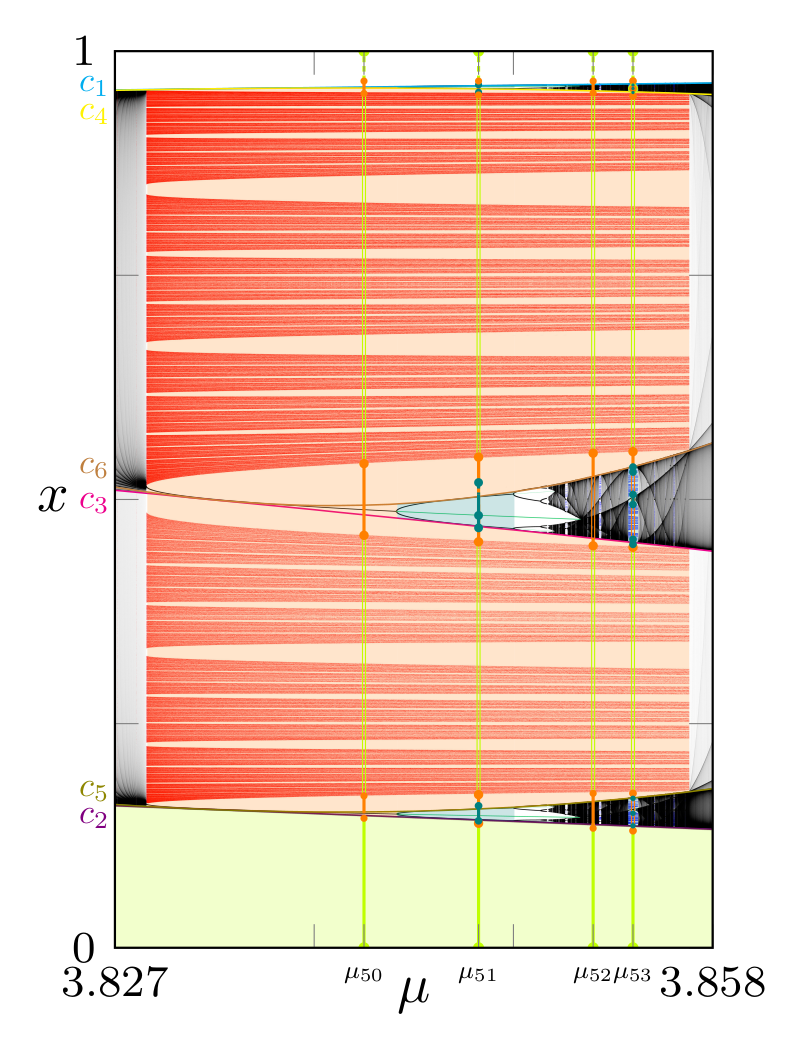
Jim Yorke, RdL, "The graph of the logistic map is a tower",
Discrete & Continuous Dynamical Systems, 41:11 (2021)

Jim Yorke, RdL, "Infinite towers in the graphs of many dynamical systems",
Nonlinear Dynamics, 105 (2021)

RdL, "Backward asymptotics in S-unimodal maps", arXiv

Happy Birthday Jim!!

Then:

If $k=p$ If $k < p$
  1. if $x\in N_p$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_p\;$;

  2. otherwise,

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_{r}$
    where $r=p-1$ or $r=p-2$.
  1. if $x\in N_k$, then

    $s\alpha(x)=N_0\cup N_1\cup\dots\cup N_k\;$;

  2. otherwise,


    where $r$ can be either $k$ or $k-1$ or $k-2$.