Section 1.1 Initial Value Problems
\begin{equation*}
f:\Bbb R\times\Bbb R^m\to\Bbb R^m
\end{equation*}
be a continuous map. By Initial Value Problem (IVP) we mean a system of first order ordinary differential equations
\begin{equation*}
x'(t) = f(t,x(t)),\;\;t\in\Bbb R,\;x(t)\in\Bbb R^m,
\end{equation*}
together with a condition
\begin{equation*}
x(t_0)=x_0
\end{equation*}
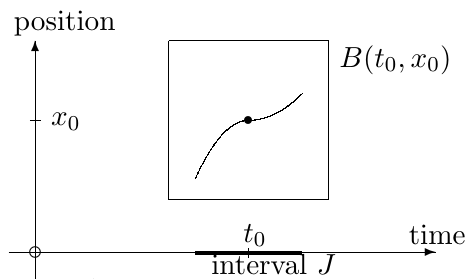
specifying the position of the desired solution at a given time. Nobody wants to waste computational time looking for solutions that do not exist. This is why the following theorem is of particular importance for the numerical analysis of IVPs: Theorem 1.1.1 (Picard, Lindelof, Cauchy, Lipschitz). Existence and uniqueness of smooth solutions.
Consider the IVP
\begin{equation*}
\dot x = f(t,x),\;\;x(t_0)=x_0.
\end{equation*}
If \(f\) is continuous for all \(t\in\Bbb R\) and uniformly Lipschitz in \(x\in\Bbb R^m\text{,}\) namely
\begin{equation*}
\|f(t,x_1)-f(t,x_2)\|\leq M \|x_1-x_2\|
\end{equation*}
for some \(M>0\) and all \(t\in\bR,\;x_1,x_2\in\Bbb R^m\text{,}\) the IVP problem above has a unique solution defined at all times \(t\) close enough to \(t_0\text{.}\)
\begin{equation*}
\dot x=x, x(t_0)=x_0
\end{equation*}
has a unique solution for all \((t_0,x_0)\text{.}\) The corresponding solution
\begin{equation*}
x(t)=x_0e^{t-t_0}
\end{equation*}
in fact is actually defined for all \(t\text{.}\)
Example 2. The rhs \(f(t,x)=x^2\) like in Example 1, is smooth for all \(t\) and \(x\text{.}\) Hence, the ODE
\begin{equation*}
\dot x=x^2, x(t_0)=x_0
\end{equation*}
has a unique solution for all \((t_0,x_0)\text{.}\) The corresponding solution
\begin{equation*}
x(t)=\frac{x_0}{1-x_0(t-t_0)},
\end{equation*}
though, blows up at \(t=t_0+1/x_0\text{.}\) Namely, as the theorem goes, the solution is defined only "for \(t\) close enough to \(t_0\)".
Example 3 The rhs \(f(t,x)=\sqrt{x}\) is smooth everywhere (in its domain) except at \(x=0\text{,}\) where \(f_x(t,x)=\frac{1}{2\sqrt{x}}\) blows up. Hence uniqueness is not granted there (for existence, continuity is enough). Indeed, in this case, there are infinitely many solutions to
\begin{equation*}
\dot x=\sqrt{x},\,x(0)=0.
\end{equation*}
For instance,
\begin{equation*}
x_1(t)=t^2/4
\end{equation*}
and
\begin{equation*}
x_2(t)=0.
\end{equation*}
