Section 1.3 Double precision
Which floating point system used in nowadays computers? Due to technical restrictions (namely we can only build miniaturized physical devices with 2 states) modern computers use base 2 to represent numbers. The standard representation for numbers is called double precision for historical reasons. The number of digits allocated for each number is \(k=52\) and the exponent ranges from \(-1022\) to \(1023\).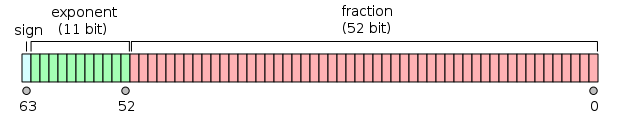
Subsection 1.3.1 Binary Numbers
Representing numbers in base 2 works exactly as in base 10, with two differences:- the only digits allowed are 0 and 1;
- a digit in position \(k\) says how many summands of \(2^k\) are in the number.
- \(1_2 = 1\times2^0 = 1\text{;}\)
- \(10_2 = 1\times2^1+0 \times2^0 = 2\text{;}\)
- \(11_2 = 1\times2^1+1 \times2^0 = 3\text{;}\)
- \(100_2 = 1\times2^2+0\times2^1+0\times2^0 = 4\text{;}\)
- \(101_2 = 1\times2^2+0\times2^1+1\times2^0 = 5\text{;}\)
- \(1000_2 = 1\times2^3+0\times2^2+0\times2^1+0\times2^0 = 8\text{;}\)
- \(1000000_2 = 1\times2^6 = 64\text{;}\)
- \(0.1_2 = 1\times2^{-1} = \frac{1}{2}=0.5\text{;}\)
- \(0.01_2 = 1\times2^{-2} = \frac{1}{4}=0.25\text{;}\)
- \(0.11_2 = 1\times2^{-1}+1\times2^{-2} = \frac{3}{4}=0.75\text{;}\)
- \(0.001_2 = 1\times2^{-3} = \frac{1}{8}=0.125\text{;}\)
- \(0.0001_2 = 1\times2^{-4} = \frac{1}{16}=0.0625\text{;}\)
- \(1.1_2 = 1\times2^{0} + 1\times2^{-1} = 1.5\text{;}\)
- \(\frac{1}{2} = 0.1_2\text{;}\)
- \(\frac{1}{3} = 0.01010101\dots_2\text{;}\)
- \(\frac{1}{4} = 0.01_2\text{;}\)
- \(\frac{1}{5} = 0.001100110011\dots_2\text{;}\)
- \(\frac{1}{6} = \frac{1}{3}\times\frac{1}{2}=0.001010101\dots_2\text{;}\)
- \(\frac{1}{7} = 0.001001001\dots_2\text{;}\)
- \(\frac{1}{8} = 0.001_2\text{;}\)
- \(\frac{1}{9} = 0.000111000111\dots_2\text{;}\)
- \(\frac{1}{10} = \frac{1}{5}\times\frac{1}{2} = 0.0001100110011\dots_2\text{;}\)
Subsection 1.3.2 Largest and smallest number in double precision
Now we are ready to evaluate the largest and smallest positive numbers representable in double precision. Largest:
\begin{equation*}
1.1\dots1_2\times2^{1023}\simeq2^{1024}\simeq1.8\times10^{308}
\end{equation*}
Smallest:
\begin{equation*}
1.0\dots0_2\times2^{-1022}\simeq2\times10^{-308}
\end{equation*}
