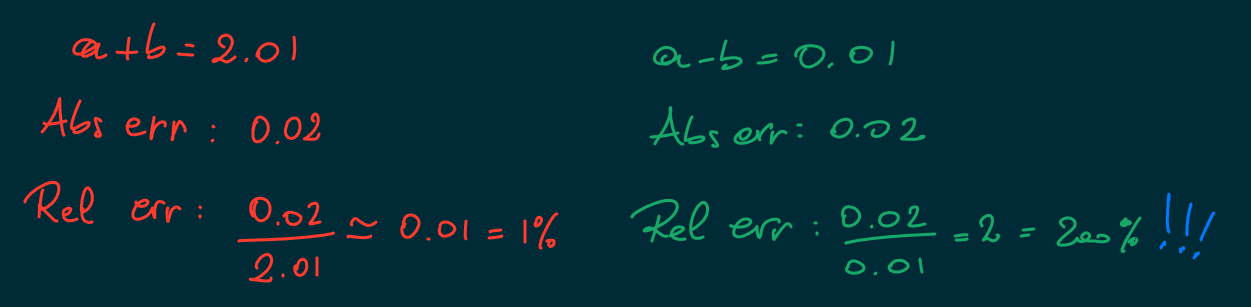Section 1.2 Floating-point Systems
Every person that studied some natural science knows how to write a number in scientific notation. For instance,
\begin{equation*}
7382.592=7.382592\times10^3
\end{equation*}
In short: we re-write each number so that only one digit appears at the left of the dot and we multiply it by a suitable power of 10 to make it equal to the original number. Floating point systems originate exactly from the convergence of two things: - the idea of scientific notation;
- the concrete fact that only a finite number of digits can be kept.
- a base, namely an integer larger than 1;
- an integer \(k\text{,}\) specifying how many digits are kept;
- a range for the exponent.
\begin{equation*}
3.83\times10^4
\end{equation*}
is a number of this system while
\begin{equation*}
3.83\times10^{-12}
\end{equation*}
is not. The largest number we can represent in \(D_3\) is
\begin{equation*}
9.99\times10^{10}\simeq10^{11}=100\;\text{billions}
\end{equation*}
The smallest positive number is
\begin{equation*}
1.00\times10^{-10}=\frac{1}{10\;\text{billions}}
\end{equation*}
Not so bad to be a toy model! The fact that each number is represented by a fixed number of digits determines a series of important consequences: Fact 1.2.1. Floating-point quirks 1.
We can have \(a+b=a\) even when \(b\neq0\text{.}\)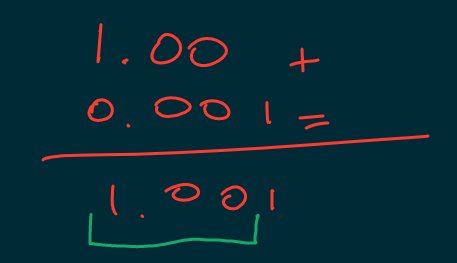
\begin{equation*}
a+b=a\;\text{!!!}
\end{equation*}
Fact 1.2.2. Floating-point quirks 2.
Equivalent formulae can give different results.
Fact 1.2.3. Floating-point quirks 3.
Subtracting two almost equal numbers is not a wise thing.