Section 1.2 Explicit Euler Method
This is the simplest numerical method to solve the IVP
\begin{equation*}
\dot x=f(t,x),\; x(t_0)=x_0.
\end{equation*}
It is just a direct consequence of Taylor`s series expansion formula:
\begin{gather*}
x(t+h) = x(t) + \dot x(t)h + \frac{\ddot x(\tau)}{2}h^2=\\
= x(t) + f(t,x(t))h + \left(f_t(\tau,x(\tau))+ f(\tau,x(\tau))f_x(\tau,x(\tau))\right)h^2
\end{gather*}
for some \(t_0\leq\tau\leq t_0+h\text{.}\) The step of the explicit Euler method is precisely
\begin{equation*}
\left\{
\begin{aligned}
x_{n+1} &= x_n + h f(t_n,x_n)\\
t_{n+1} &= t_n+h\\
\end{aligned}\right.
\end{equation*}
Local error. The local error of a single-step ODE method, such as the Euler method, is the quantity
\begin{equation*}
x_{n+1} - x(t_n+h),
\end{equation*}
where \(x(t)\) is the solution of the IVP
\begin{equation*}
\dot x=f(t,x),\; x(t_n)=x_n.
\end{equation*}
Looking at the Taylor expansion above, the local error of the Euler methos is of order 2, namely it goes to zero as \(h^2\text{.}\)
A numerical example. Below is an implementation of the Euler method used to evaluate numerically \(x(25)\) for the solution of the IVP
\begin{equation*}
\begin{aligned}
&\dot x = -x\cos t\\
&x(0)=1,\\
\end{aligned}
\end{equation*}
whose analytical solution (use separation of variables!) is
\begin{equation*}
x(t) = e^{-\sin t}\,.
\end{equation*}
Euler method \(\Longleftrightarrow\) left Riemann sums. When \(f\) depends on \(t\) only,
\begin{equation*}
\begin{aligned}
x_1 &= x_0 + hf(t_0)\\
x_2 &= x_0 + hf(t_0) + hf(t_0+h)\\
\dots&\\
x_n &= x_0 + hf(t_0) + hf(t_0+h) + \dots + hf(t_0+(n-1)h),\\
\end{aligned}
\end{equation*}
namely
\begin{equation*}
x_n-x_0 = \left[f(t_0) + f(t_0+h) + \dots + f(t_0+(n-1)h)\right]h
\end{equation*}
(compare with the left Riemann sum formula in https://deleo.website/NumericalAnalysis/sec-integrals.html)
Global error. By running the code above with different values of \(N\text{,}\) one can guess easily the global order of the Euler method.
When the rhs \(f(t,x)\) does not depend on \(x\text{,}\) we know already that the method is of order 1 (see https://deleo.website/NumericalAnalysis/sec-integrals.html). What to do when it does depend on \(x\text{?}\) In this case, we cannot take the maximum of \(|f(t,x)|\) because there is no way to know the range of \(x(t)\text{!}\) We need a new argument. Let \(x(t)\) be the exact solution of the ODE and set
\begin{equation*}
e_n = x(t_n)-x_n.
\end{equation*}
Then
\begin{gather*}
e_{n+1} = x(t_{n+1})-x_{n+1} = \\
= x(t_n)+\dot x(t_n)h+\frac{\ddot x(\tau)}{2}h^2-\left(x_n+f(t_n,x_n)h\right)=\\
= e_n+(f(t_n,x(t_n))-f(t_n,x_n))h+\frac{\ddot x(\tau)}{2}h^2.
\end{gather*}
The last term is the local truncation error, so we know that there is a constant \(M\) such that this error is bound from above by \(Mh^2\text{.}\) Moreover, we are assuming that \(f(t,x)\) is uniformly Lipschitz in the second argument, so there is some constant \(K\text{,}\) independent on \(t\text{,}\) such that
\begin{equation*}
\|f(t_n,x(t_n))-f(t_n,x_n)\|\leq K\|x(t_n)-x_n\|=Ke_n.
\end{equation*}
Hence,
\begin{equation*}
\|e_{n+1}\| \leq \|e_n\|(1+Kh)+\frac{M}{2}h^2,
\end{equation*}
so that
\begin{equation*}
\|e_1\|\leq\frac{M}{2}h^2
\end{equation*}
and
\begin{equation*}
\|e_{n}\|\leq\|e_{n-1}\|\cdot(1+Kh)\leq\dots\leq\|e_{1}\|\cdot(1+Kh)^{n-1}.
\end{equation*}
Hence
\begin{equation*}
\|e_{1}\|+\dots+\|e_N\|\leq\|e_{1}\|\left((1+Kh)+\dots+(1+Kh)^{n-1}\right)\leq
\end{equation*}
\begin{equation*}
\leq\frac{M}{2}h^2\frac{(1+Kh)^N-1}{Kh}=Ah,
\end{equation*}
where
\begin{equation*}
A=M\frac{e^{K(t_f-t_0)}-1}{2K}
\end{equation*}
is a bounded constant. This proves that the Euler method has global error order 1, namely 1 less than its local error order.
Round-off error. Recall that every numerical method is affected by two sources of error: - a truncation error, depending on the approximations on which the method is based;
- a round-off error, due to the use of floating-point arithmetic.
\begin{equation*}
x_{n+1} = x_n + h f(t_n,x_n)
\end{equation*}
and that, in a sum, the absolute errors sum up. Since \(h\) is usually quite small with respect to \(x_n\text{,}\) we have that the round-off absolute error on \(x_{n+1}\) is of the order of
\begin{equation*}
|x_n|\epsilon_m\,,
\end{equation*}
where \(\epsilon_m\) is the "epsilon-machine" value. Consider, by simplicity, a case when the \(x_n\) are all of the same order of magnitude. Then the round-off error will contribute to the global error of the Euler explicit method by an amount bound from above by something of the order
\begin{equation*}
\sum_{n=1}^N|x_n|\epsilon \simeq N C \epsilon \simeq \frac{C'}{h}\,,
\end{equation*}
since the number of steps \(N\) of the method is proportional to \(1/h\) and, in the worst case scenario, the errors will all have the same sign. Hence, an upper bound for the global error of the Explicit Euler method has the following expression:
\begin{equation*}
e(h) = \frac{C}{h}+C'h\,,
\end{equation*}
just as in case of the numerical estimate of the derivative with forward differencing. We expect therefore the following picture: 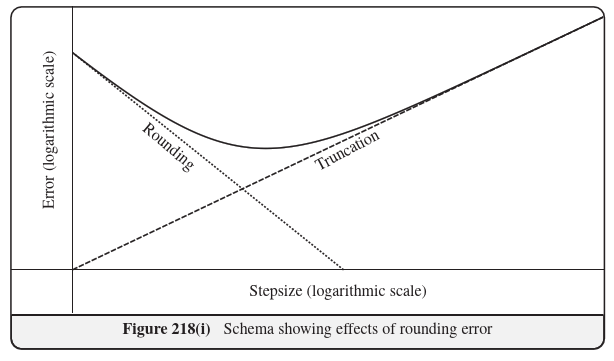
\begin{equation*}
\dot x = -x\cos t,\;x(0)=1.
\end{equation*}
In order to see the floating point error, we need to work in single precision since otherwise the calculations would take too long and online "too long" calculations are not allowed.
