Discrete Dynamical Systems

Keywords: Logistic Map, Graph of a Dynamical System, Chain-Recurrence, Lorenz System

Several discussions with Jim Yorke about the qualitative dynamics of Real Newton Maps led us to study a common interest, the qualitative dynamics of the logistic map nearby its chain-recurrent set. Notice that, for almost all parameters, chain-recurrent points coincide with the non-wandering ones. The qualitative difference between the Chain-recurrent set $R$ and the non-wandering set $\Omega$ is that $R$, unlike $\Omega$, comes with a natural equivalence relation and so its sets are naturally sorted into subsets that we call nodes.

Following C. Conley's idea of encoding the qualitative behavior of a dynamical systems into a graph, we studied the graph of one of the simplest non-trivial and well known discrete dynamical system, namely the logistic map $$ \ell_\mu(x) = \mu x(1-x). $$ The nodes of the graph are the equivalence classes of chain-recurrent points and there is an edge from node $A$ to node $B$ if there is some point $x$ whose $\omega$-limit is contained in $B$ and such that there is a backward trajectory based at $x$ whose limit is contained in $A$.

Notice that, since there can be no loop in the graph of a Dynamical System (due to the existence of a global Lyapunov function), this means that in a tower nodes can be ordered linearly as $N_0,N_1,\dots,N_p$, where possibly $p=\infty$, so that there is an edge from $N_0$ to any other node, there is an edge from $N_1$ to any other node but $N_0$ and so on. In particular, there is no edge coming out form $N_p$ and every node $N_i$, $i\neq p$, has an edge to $N_p$. In terms of dynamics, this means that points arbitrarily close to $N_0$ can asymptote to every other node, while points arbitrarily close to $N_1$ can asymptote to every other node except $N_0$ and so on.

Ultimately, we were able to prove the following result:

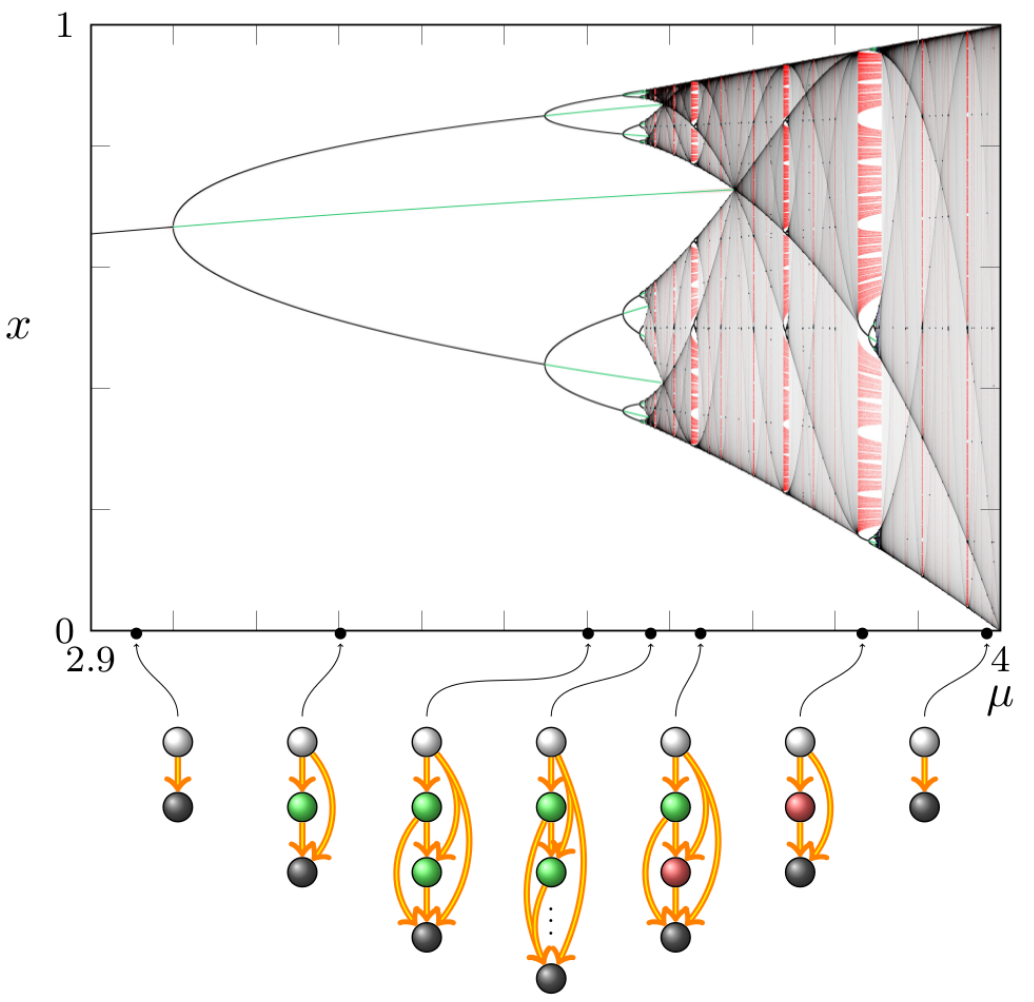
Examples of graphs of the logistic map for different values of the parameters are shown in the figure below. The white node is the fixed point $x=0$. Green nodes are repelling periodic orbits. Red nodes are repelling Cantors sets. Black nodes are attractors (recall that the logistic map has a unique attractor for every $\mu$).

Notice that for certain parameter values there are infinitely many repellors. This is the case, for instance, of the Feigenbaum-Myrberg parameter, where each repellor is an unstable $2^k$-cycle for $k=1,2,\dots$ and the attractor is a Cantor set on which the map acts as an adding machine (see the middle tower in the picture above).

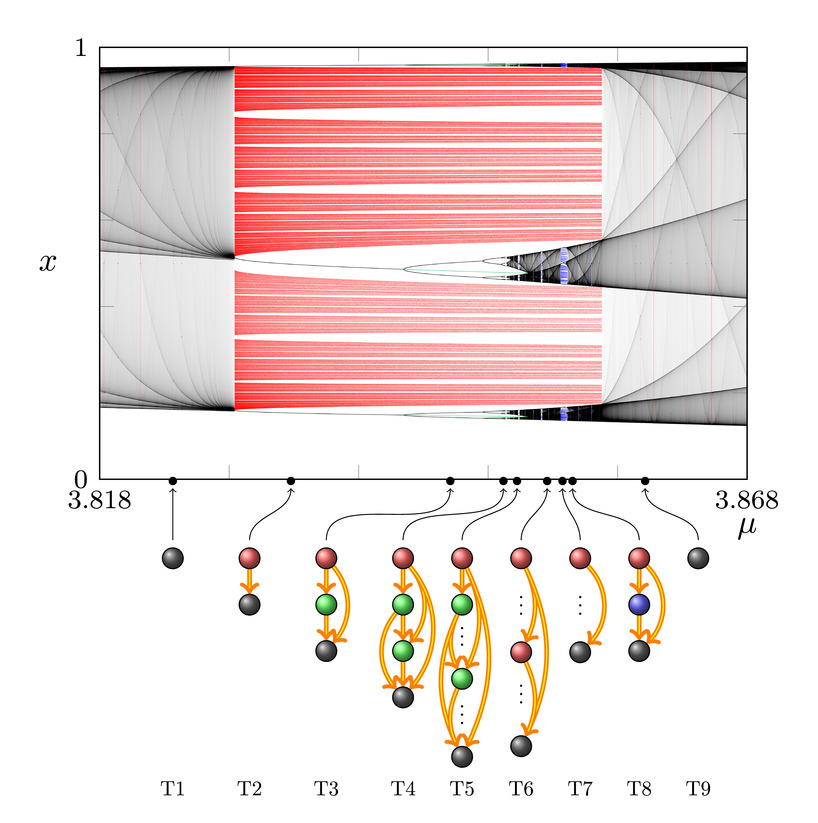
In order to provide evidence that our findings for the logistic map actually appear also in completely unrelated systems in higher dimension, we studied numerically the Lorenz system. Below we show a picture of the bifurcation diagram for the period-3 window of the logistic map followed by a detail of the bifurcation diagram of a Poincare' map of the Lorenz system.

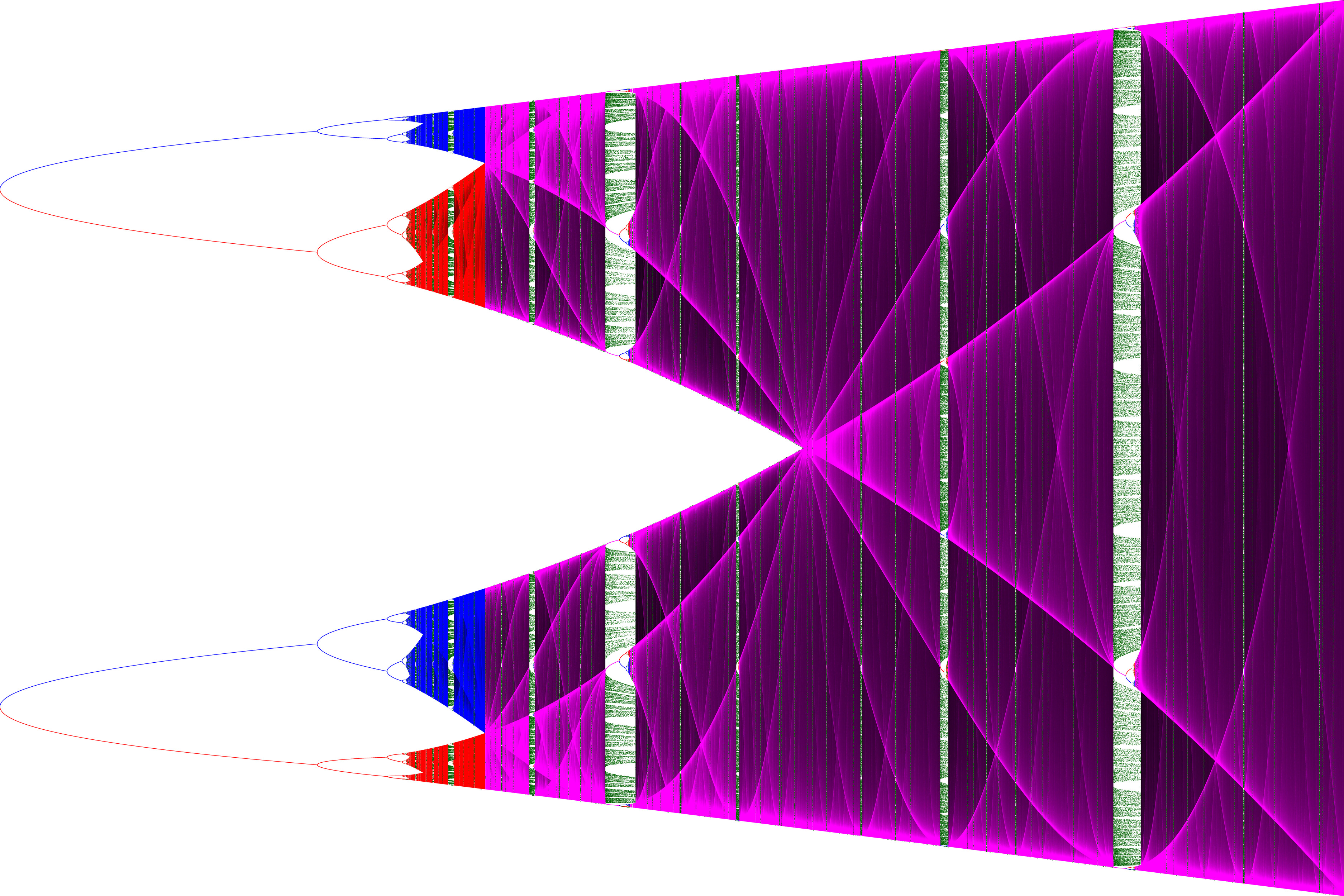
Next picture shows the bifurcation diagram of a bimodal map. The strcture of the graph of S-multimodal maps has not been studied yet.

See the articles below for more details, results and examples:

• R. De Leo and J. Yorke, The graph of the logistic map is a tower, Discrete and Continuous Dynamical Systems, 41:11 (2021).
• R. De Leo and J. Yorke, Infinite towers in the graph of a dynamical system, Nonlinear Dynamics, 105 (2021).
• R. De Leo, Backward asymptotics in S-unimodal maps, accepted for pubication on the Internation J. of Bifurcations and Chaos (2022).