Real Newton Fractals

See the Gallery for high-resolution versions of the published pictures and many other pictures and videos I could not include in the publications.

Keywords: Newton algorithm, Fractals, Julia set, $\alpha$-limit, Barna's Theorem

About 100 years ago, Fatou and Julia started the study of the discrete dynamics of rational complex maps. Newton's root-finding method applied to complex functions provides an interesting subclass of such rational maps:

Theorem [Head, 1988]. Every complex rational map $R(z)$ of degree $d$ with $d$ distinct superattracting fixed points is conjugate, via a Mobius transformation, to the Newton's map $$N_p(z)=z-\frac{p(z)}{p'(z)}$$ of a complex polynomial $p(z)$ of degree $d$. If $\infty$ is fixed but not superattracting, then $R=N_p$.

Correspondingly, their Julia and Fatou sets have special properties. In particular:

The Julia set $J$ of $N_p$ is connected and has empty interior;
All components of the Fatou set $F$ of $N_p$ are simply connected and all immediate basins of the roots $r_i$ of $p$ are unbounded;
If the only attractors of $N_p$ are the roots $r_i$ of $p$, then the $\alpha$-limit of $r_i$ of $p$ is $J\cup\{r_i\}$ for each root $r_i$ and the $\alpha$-limit of any other point is $J$.

The figure below shows the Fatou set of the Newton map of the polynomial $p(z)=z^3-1$ (left) and its Julia set obtained as $\alpha$-limit of a non-root point (right).

Given the rich behavior of holomorphic Newton maps on $\mathbb R^2$, it is natural to ask what happens in case of non-holomorphic ones, namely Newton maps of polynomial maps of $\mathbb R^2$ into itself. Quite surprisingly, very few articles has been dedicated to this topic so far: a few in the 80s by a group led by H. Peitgen and one by Yorke and Miller in 2000. That is why I decided to start the analytical and numerical study of this field.

A starting point for this field is the following theorem on Newton maps of polynomials on the real line:

Theorem [Barna, 1953]. Let $p$ be a generic real polynomial of degree $n\geq4$ without complex roots. Let $r_1,\dots,r_n$ be the roots of $p$ and $N_p$ its Newton polynomial. Then:

The Fatou set of $N_p$ has full measure and is the union of the basins of attraction of the roots of $p$;
$N_p$ has no attracting $k$-cycles for $k\geq2$;
$N_p$ has repelling cycles of any order $k\geq2$;
The Julia set of $N_p$ is the union of a countable set and a Cantor set of measure zero.

Based on the numerical exploration of many cases and in agreement with analytical results in some simple case, I formulated the following conjecture:

Conjecture [DL, 2019]. Let $p$ be a generic polynomial map of $\mathbb R^2$ in itself of degree $n\geq3$ with $n$ simple roots $r_1,\dots,r_n$. Then:

The Fatou set of $N_p$ has full measure and is the union of the basins of attraction of the roots of $p$;
The Julia set $J_p$ of $N_p$ is the countable union of wedge sums of countably many circles and of a Cantor sets of circles of measure zero.
There is a non-empty open set of points whose $\alpha$-limit is the set of non-regular points of $J_p$.

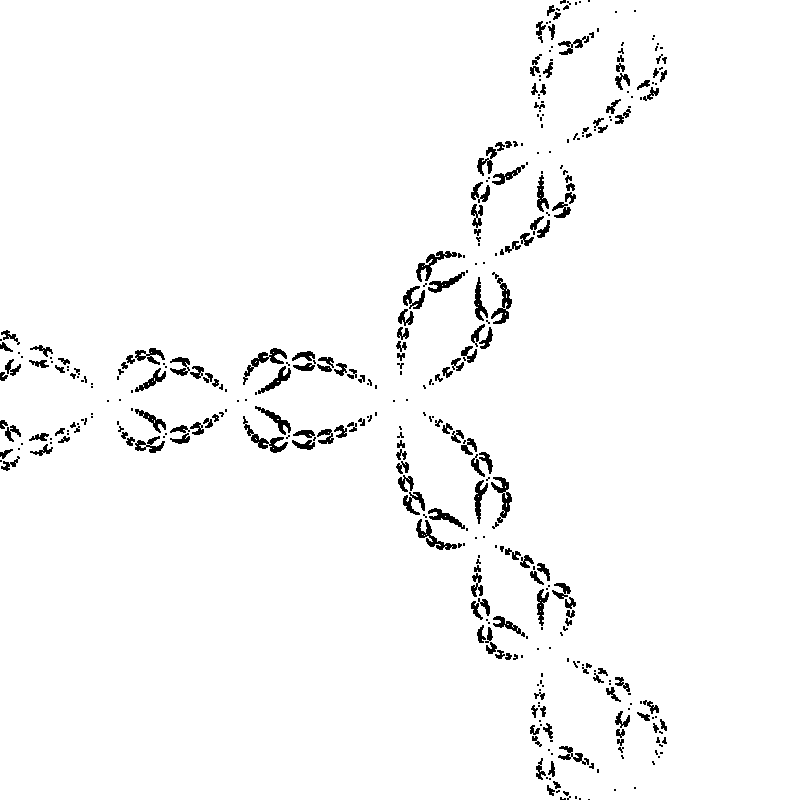
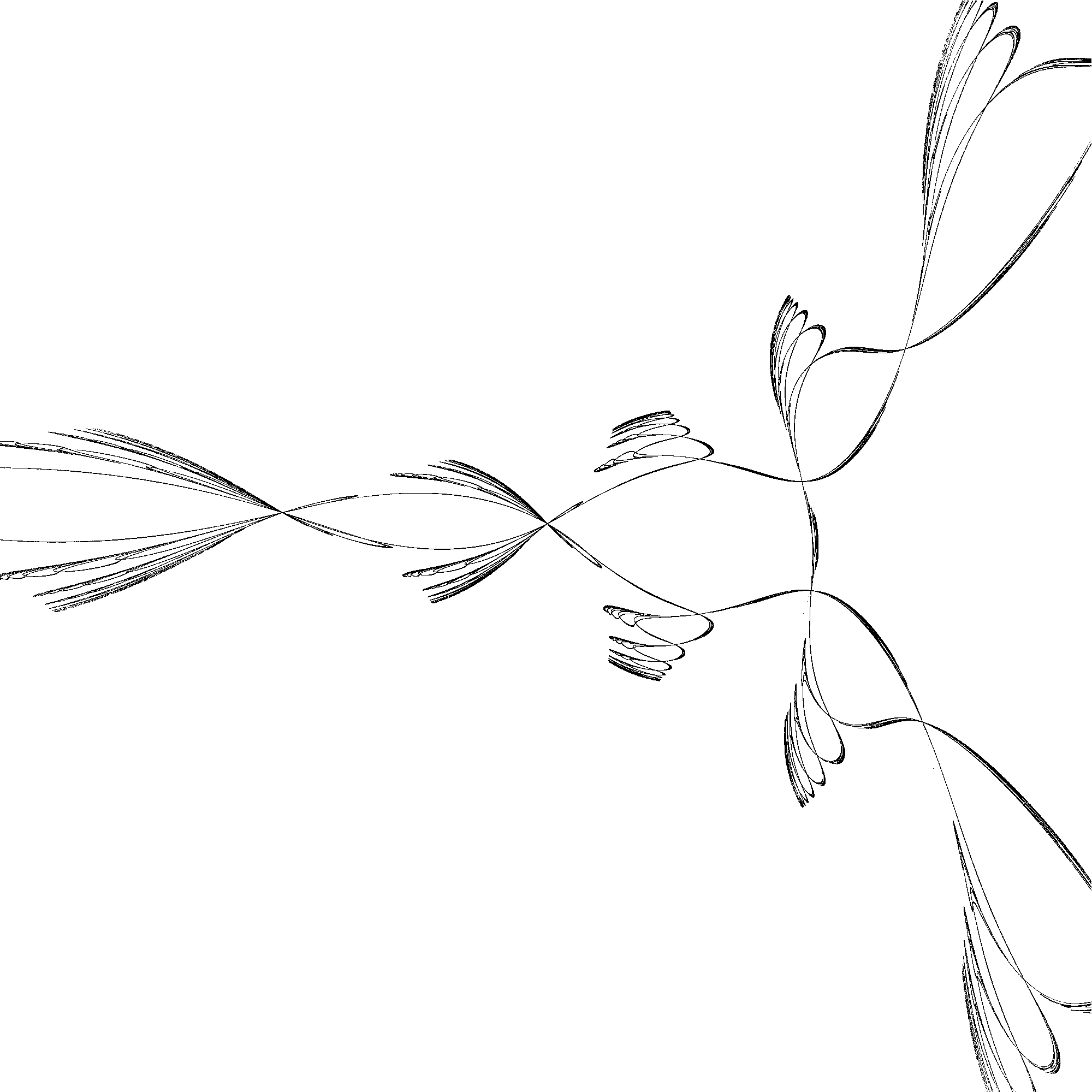
The figure below shows an example where the conjecture appear to work: the Newton map of the polynomial map $p(x,y)=(xy-1,(x-5)^2-y^2-1)$, that has maximal number (i.e. four) of real roots. The left picture shows the basins of attraction of the four roots of the map; the picture at the right shows the $\alpha$-limit of the point $(-10,-3.6)$.

See the articles below for more details, results and examples:

R. De Leo, Conjectures about simple dynamics for some real Newton maps on R², Fractals, 27:6 (2019).
R. De Leo, Julia sets of Newton maps of real quadratic polynomial maps on the plane, Internation J. of Bifurcations and Chaos, 30:9 (2020).