Cohomological Equation
Keywords: Partial Differential Equations , Weak solutions , non-Hausdorff manifolds , Foliations , Almost-Complex structures , Symplectic Geometry
The main goal of this research field is finding solvability conditions
for the simplest non-trivial PDE on the plane.
This PDE is the so-called Cohomological Equation
$$Xf=g,$$
where $X=a(x,y)\partial_x + b(x,y)\partial_y$ is a planar vector field
without zeros, namely $a^2+b^2>0$, and $g$ is a $C^k$ function for some $k=0,1,\dots$
In the non-trivial case, the space $F$ of the integral trajectories of $X$ is non-Hausdorff and the
solvability of the relative Cohomological Equation is related to the differential structure of $F$.
In order to illustrate a concrete example, we call a set $U$ saturated if it is the union of trajectories of $X$.
Two integral trajectories $t_1,t_2$ are said inseparable, and are called separatrices, when every saturated neighborhood $U_1$ of $t_1$
intersects every saturated neighborhood $U_2$ of $t_2$.
Then, when
$$
X(x,y) = 2y\partial_x+(1-y^2)\partial_y,
$$
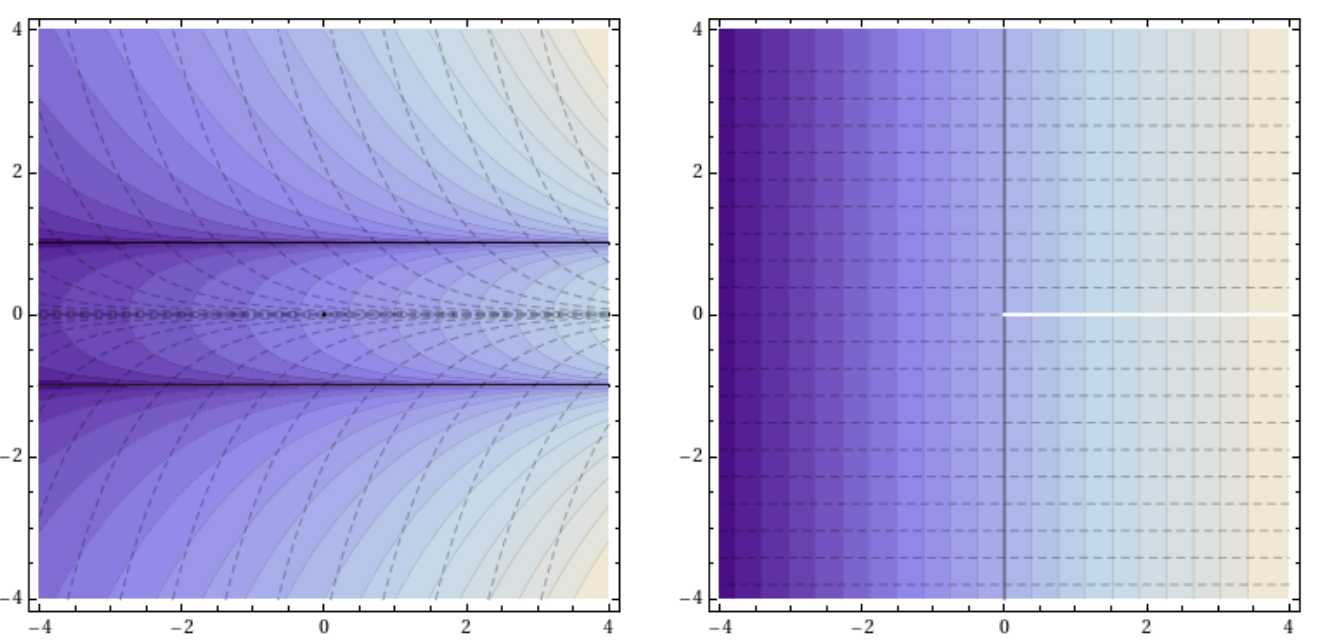
the two horizontal lines $y=\pm1$ are integral trajectories of $X$ and are separatrices (see the left figure below).
In this case, the space $F$ is, literally, a "$Y$", namely a manifold consisting in two real lines with the two negative half-lines
identified. In particular, the two origins are inseparable in the induced quotient topology and correspond to the
two separatrices mentioned above.
One of my main results is the existence of normal coordinates for this problem. More precisely, I proved that in each saturated neighborhood of any two contiguous separatrices,
it is possible to find coordinates so that the PDE writes simply as
$$
\partial _y f'=g'
$$
over the open set $\Omega=\mathbb R^2\setminus[0,\infty)$ (see the right figure above).
In the example above, a set of normal coordinates -- the ones used in the right figure above -- is given by
$$
x'=(y^2-1)e^x,\;\;\; y'=-2y e^x.
$$
Note that, as suggested in the figure, the image of the plane in the accented coordinates is the complement
of the positive $x$ semiaxis. The two separatrices in the left figure map respectively, in the right figure,
to the two half-lines $x'=0, y'>0$ and $x'=0, y'<0$.
See the articles below for more details, results and examples:
One of my main results is the existence of normal coordinates for this problem. More precisely, I proved that in each saturated neighborhood of any two contiguous separatrices,
it is possible to find coordinates so that the PDE writes simply as
$$
\partial _y f'=g'
$$
over the open set $\Omega=\mathbb R^2\setminus[0,\infty)$ (see the right figure above).
In the example above, a set of normal coordinates -- the ones used in the right figure above -- is given by
$$
x'=(y^2-1)e^x,\;\;\; y'=-2y e^x.
$$
Note that, as suggested in the figure, the image of the plane in the accented coordinates is the complement
of the positive $x$ semiaxis. The two separatrices in the left figure map respectively, in the right figure,
to the two half-lines $x'=0, y'>0$ and $x'=0, y'<0$.
See the articles below for more details, results and examples:
- R. De Leo, T. Gramtchev and A. Kirilov, Global Solvability in Functional Spaces for Smooth Nonsingular Vector Fields in the Plane, in "Pseudo-Differential Operators: Analysis, Applications and Computations", L. Rodino, M.W. Wong and H. Zhu eds., Springer (2011), ISBN 978-3-0348-0048-8, arXiv:1001.2121v1
- R. De Leo, Solvability of the cohomological equation for regular vector fields on the plane, Annals of Global Analysis and Geometry, 39:3, 231-248, 2011, arXiv:1007.3016v1
- R. De Leo, Weak solutions of the cohomological equation in the plane for regular vector fields, Mathematical Physics, Analysis and Geometry, 18:18, 2015, manuscript