Section 3.3 Newton's method
The bisection method is very low-demanding: as long as a function is continuous, the method does work and the error decreases linearly. We can improve the convergence speed by requiring for more regularity: if we are close enough to a root \(r\) of \(f(x)\), the derivative of \(f\) can be used to get closer and closer to \(r\)!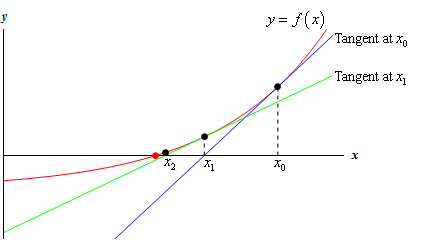
Subsection 3.3.1 The algorithm
Given an initial point \(x_0\text{,}\) the equation of the line tangent to the graph of \(f(x)\) passing through \((x_0,f(x_0))\) is
\begin{equation*}
y-f(x_0) = f'(x_0)(x-x_0)
\end{equation*}
This line cuts the \(y\) axis at
\begin{equation*}
x = x_0 - \displaystyle\frac{f(x_0)}{f'(x_0)}
\end{equation*}
Denote this new point by \(x_1\text{.}\) Repeating this procedure recursively, we come up with points
\begin{equation*}
x_2 = x_1 - \displaystyle\frac{f(x_1)}{f'(x_1)},
\end{equation*}
\begin{equation*}
x_3 = x_2 - \displaystyle\frac{f(x_2)}{f'(x_2)}
\end{equation*}
and so on. This leads to Newton's algorithm:
\begin{equation}
x_n = x_{n-1} - \displaystyle\frac{f(x_{n-1})}{f'(x_{n-1})}\label{eq-Newton}\tag{3.3.1}
\end{equation}
Subsection 3.3.2 Does it work?
The sequence \(x_0,x_1,x_2,\dots\) does not converge necessarily (I'll show an example below) but if it does, then it does converge to a root. Indeed, assume that \(\lim x_n=r\). Then, provided that \(f\) and \(f'\) are continuous and that \(f'(r)\neq0\text{,}\)
\begin{equation*}
r = \lim x_n = \lim x_{n-1} - \lim \displaystyle\frac{f(x_{n-1})}{f'(x_{n-1})} = r - \displaystyle\frac{f(r)}{f'(r)}
\end{equation*}
and so \(f(r)=0\). Moreover, it can be proved that Newton's method always converges when \(x_0\) is taken "close enough" to \(r\text{.}\)Subsection 3.3.3 We are requiring more regularity to \(f\text{,}\) is it worth?
Unlike the bisection method, Newton's method require the existence and continuity of \(f'\text{.}\) So why do we like it anyway? Speed! The error \(e_n=x_n-r\) in the Newton's method decreases quadratically!
\begin{equation*}
e_n = x_n-r = x_{n-1}-\displaystyle\frac{f(x_{n-1})}{f'(x_{n-1})} - r = e_{n-1} - \displaystyle\frac{f(x_{n-1})}{f'(x_{n-1})}
\end{equation*}
Recall Taylor series:
\begin{equation*}
f(x_{n-1}) = f(r) + f'(r)(x_{n-1}-r) + \frac{f''(s)}{2}(x_{n-1}-r)^2
\end{equation*}
Hence
\begin{equation*}
e_n = \frac{f''(s)}{2f'(r)}e^2_{n-1}
\end{equation*}
In short, one expresses this relation as
\begin{equation*}
e_n = O(e_{n-1}^2)
\end{equation*}
This means that, as soon as \(e_n\) becomes of the order of \(10^{-1}\text{,}\) the number of exact digits doubles at every step!Subsection 3.3.4 An implementation of the Newton's algorithm
The code below evaluates the square root of 2 with Newton's method. The mthod needs in input an initial value \(x_0\text{,}\) a function \(f\) and its derivative \(f'\text{.}\)Subsection 3.3.5 Problems of the Newton's algorithm
We point out typical situations when Newton's algorithm fails. 1. If the starting point \(x_0\) is chosen "too far" from the root, the algorithm might not converge to it. For instance, consider \(f(x)=x^2-2\text{,}\) so that Newton's algorithm is
\begin{equation*}
x_{n+1} = x_n - \frac{x_n^2-2}{2x_n} = \frac{x_n^2+2}{2x_n}.
\end{equation*}
Suppose we are looking for the positive root. From the algorithm is clear that, if \(x_0<0\text{,}\) all \(x_n\) will be negative too and so in particular will not converge to \(\sqrt{2}\text{.}\) In this case, indeed, it is easy to show that \(x_n\) will converge to \(\sqrt{2}\) if \(x_0>0\) and to \(-\sqrt{2}\) if \(x_0<0\text{.}\) What happens when \(x_0=0\text{?}\)
2. The continuity of the derivative nearby the zero is necessary to grant the convergence of the algorithm to the root for starting points close enough to it. For instance, the function
\begin{equation*}
f(x) = \sgn(x)\sqrt{|x|}
\end{equation*}
has a single root, the point \(x=0\text{.}\) In that point, though, the derivative diverges and so is not continuous. Newton's algorithm applied to \(f\) gives
\begin{equation*}
x_{n+1} = x_n - \frac{\sgn(x_n)\sqrt{|x_n|}}{1/(2\sqrt{|x_n|)}} = x_n - 2\sgn(x_n)|x_n|=-x_n.
\end{equation*}
Hence, no matter which starting point \(x_0\neq0\) one takes, the sequence won't converge to anything but rather will oscillate forever between \(x_0\) and \(-x_0\text{.}\)
3. A last thing that can go wrong is visible from the algorithm formula (3.3.1): when a term \(x_n\) is a critical point of the graph of \(f\text{,}\) namely \(f'(x_n)=0\text{,}\) the algorithm fails. This is the case, for instance, of the example in case 1 for \(x_0=0\text{.}\)