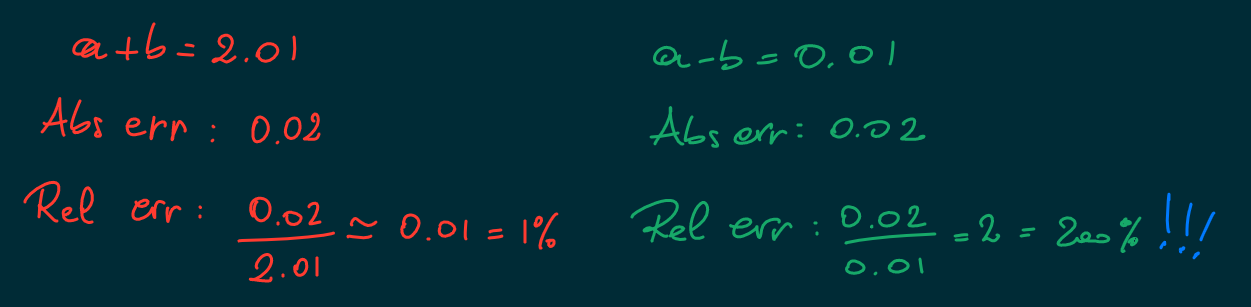NA Floating-point Systems

Section 1.2 Floating-point Systems

Every person that studied some natural science knows how to write a number in scientific notation. For instance,

\begin{equation*} 7382.592=7.382592\times10^3 \end{equation*}

In short: we re-write each number so that only one digit appears at the left of the dot and we multiply it by a suitable power of 10 to make it equal to the original number.

Floating point systems originate exactly from the convergence of two things:

the idea of scientific notation;
the concrete fact that only a finite number of digits can be kept.

In a floating point system, for each number whose exponent, in scientific notation, is in the allowed range, are kept just some fixed number of digits $k\text{.}$

In particular, every floating point system is characterized by:

a base, namely an integer larger than 1;
an integer $k\text{,}$ specifying how many digits are kept;
a range for the exponent.

A toy model. Throughout this section we will use the following simple floating point system that we denote by $D_3$: we keep only 3 (decimal) digits and we allow exponents in the range $-10,\dots,10\text{.}$

Hence,

\begin{equation*} 3.83\times10^4 \end{equation*}

is a number of this system while

\begin{equation*} 3.83\times10^{-12} \end{equation*}

is not.

The largest number we can represent in $D_3$ is

\begin{equation*} 9.99\times10^{10}\simeq10^{11}=100\;\text{billions} \end{equation*}

The smallest positive number is

\begin{equation*} 1.00\times10^{-10}=\frac{1}{10\;\text{billions}} \end{equation*}

Not so bad to be a toy model!

The fact that each number is represented by a fixed number of digits determines a series of important consequences:

Fact 1.2.1. Floating-point quirks 1.

We can have $a+b=a$ even when $b\neq0\text{.}$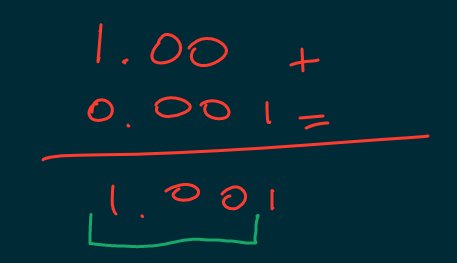

For instance, in $D_3$ take $a=1.00$ and $b=1.00\times10^{-3}\text{.}$

\begin{equation*} a+b=a\;\text{even though $b\neq0$!!!} \end{equation*}

Fact 1.2.2. Floating-point quirks 2.

Equivalent formulae can give different results.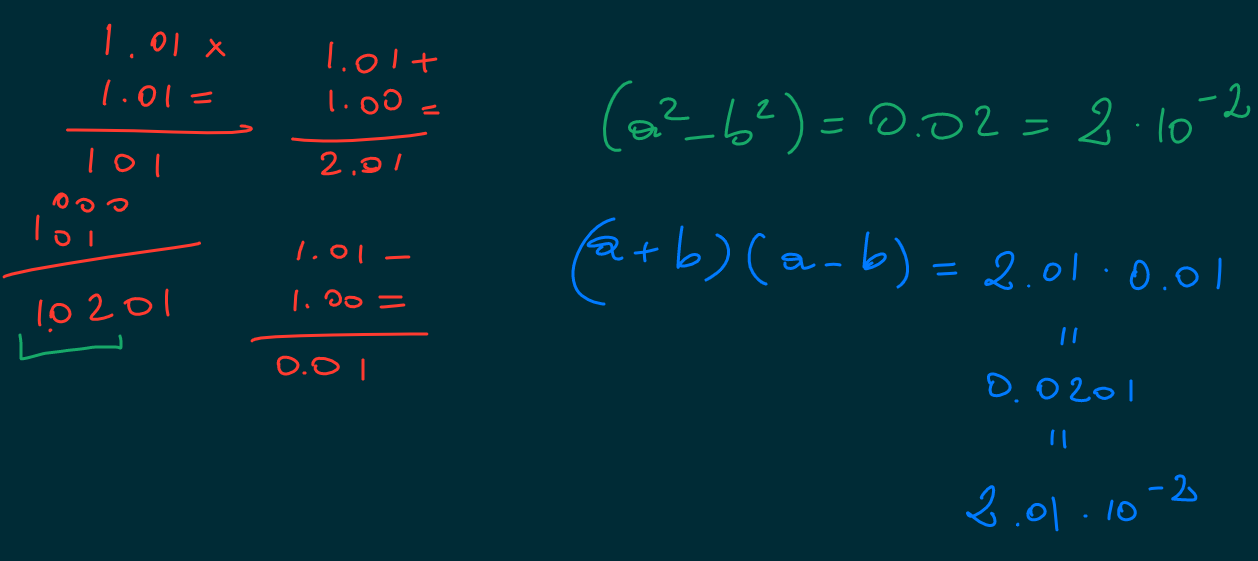

For instance, in $D_3$ take $a=1.01$ and $b=1.00$ and let us evaluate $a^2-b^2$ and $(a+b)(a-b)\text{.}$

Fact 1.2.3. Floating-point quirks 3.

Subtracting two almost equal numbers is not a wise thing.

For instance, in $D_3$ take again $a=1.01$ and $b=1.00\text{.}$ Recall that, due to round-off, we must always assume an error of $1$ on the last digit of $a$ and $b\text{.}$ Let us evaluate the absolute and relative errors of the sum and difference of these two numbers:

The three problems shown above are not particular quirks of $D_3$ but are rather a common feature of every floating point system and you should always keep them in mind when making your numerical calculations!!