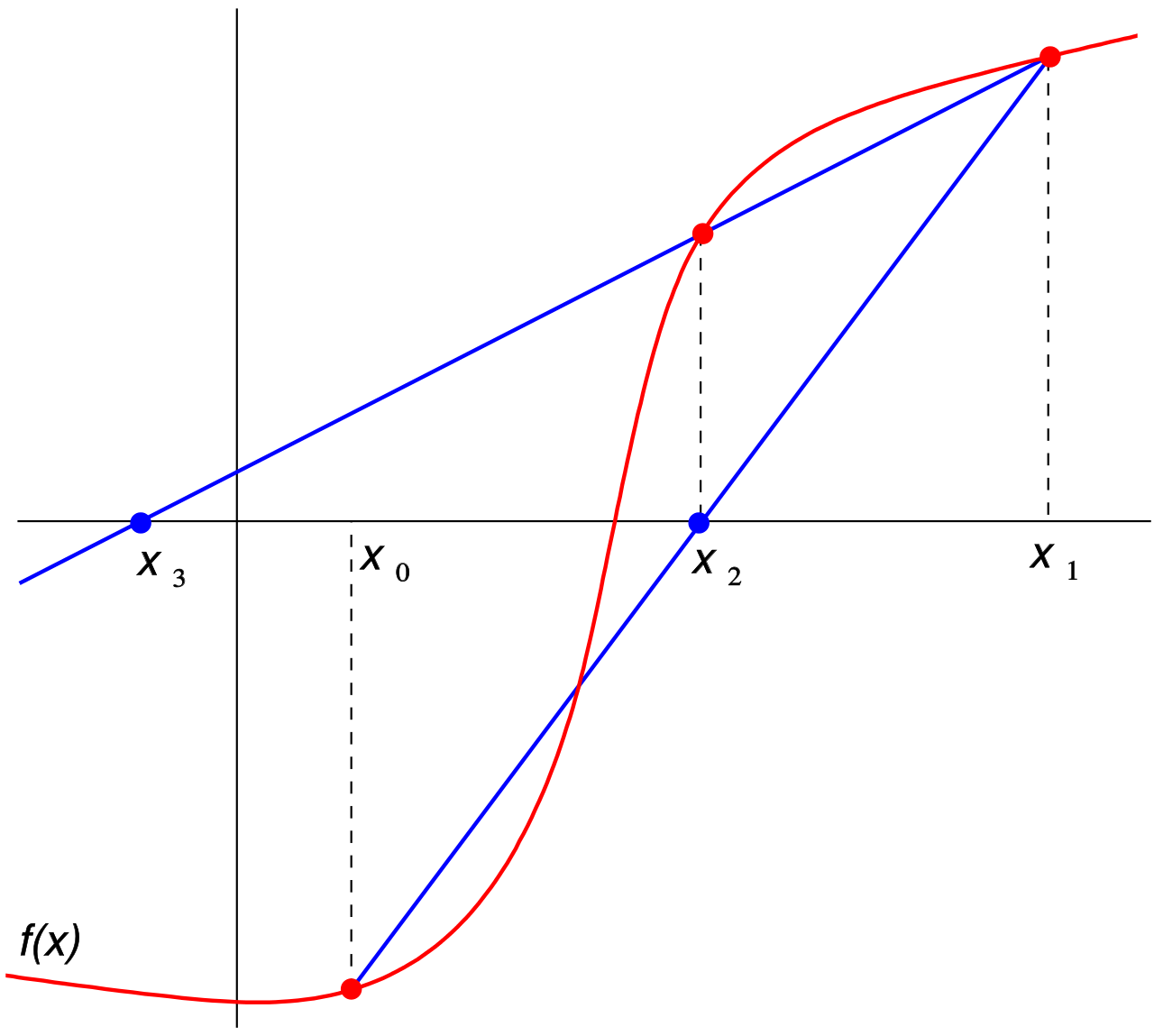
Section 3.5 Secant method
Newton's method algorithm suggests a change that would make it again work, at least in principle, for maps that are just continuous: replacing \(f'(x_n)\) by its elementary approximation
\begin{equation*}
\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}\text{,}
\end{equation*}
we get the so-called secant method:
\begin{equation*}
x_{n+1} = x_{n} - \displaystyle\frac{f(x_{n})}{\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}} = x_{n} - \displaystyle f(x_n)\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}.
\end{equation*}
\begin{equation*}
e_n = O(e_{n-1}^\phi),
\end{equation*}
where \(\phi=(1+\sqrt{5})/2\simeq1.6\) is the so-called golden ratio.
An implementation of the secant algorithm. The code below evaluates the square root of 2 with the secant's method. The algorithm needs in input two initial values \(x_0\) and a function \(f\text{.}\)
A more robust implementation. So far in our code we did not check for any "bad thing" thast can happen. For instance, in the code above we get a "division by zero" warning because, after a few steps, the algorithm saturates all significant digits of the solution and so \(x_0\) and \(x_1\) become equal and so the evaluation of the slope in line 7 fails. We can avoid this kind of problems by replacing the fixed loop <for i in range(10)> by a while loop that ends when the distance between \(x_n\) and \(x_{n-1}\) becomes smaller than some given positive number \(\epsilon\) (the desired relative precision) multiplied by \(x_n\text{:}\) 