Appendix A Can we trust the accuracy of functions evaluations on computers?
Let us see first an example of how functions are evaluated by computers. In concrete, we will give a look to the sine function.
How functions are evaluated on a computer. As mentioned in Section 2.1, functions can be evaluated via Taylor series. The code below implements the Taylor series for the sine function with 6 non-zero terms (namely up to the term of order 13) and compares some of its values with the corresponding values of the math.sin function.
It turns out that usually no single algorithm is good enough to evaluate numerically a function. For instance, the code below shows that evaluating the sine function for large angles close to \(2k\pi\) for some integer \(k\) increases the error by an order of \(k\cdot\varepsilon_m\) (namely \(k\) significant digits are lost).
The following concerete example shows why the evaluation of trigonometric functions at points near to large angles almost equivalent to zeros of the function is problematic. Consider the angle \(x = 8248.251512\) and let us reduce it to an angle in the \([-\pi/2,\pi/2]\) interval:
\begin{equation*}
x = x^* + 1313\times2\pi -\frac{\pi}{2} = x^* + 5251\times\frac{\pi}{2}
\end{equation*}
for
\begin{equation*}
x^*=-2.14758367...\times10^{-12}.
\end{equation*}
Let us see what happens in a decimal floating point systems with 10-digits mantissa:
Therefore, in D10,
\begin{equation*}
x^*=8248.251512-8248.251513 = -1\times10^{-6}.
\end{equation*}
The value of \(x^*\) in D10 is wrong by 6 orders of magnitude, and so will be the value of the sine of that angle!!
A real-world software implementation of the sine function. The C code below is the implementation of the sine function used in the GNU implementation of C language on Linux since October 2011:
- When \(|x|<2^{-26}\text{,}\) either an underflow error is reported (when the angle is so small that cannot be represented in double precision) or the value of \(\sin x\) is approximated by its Taylor polynomial of order 1, namely the approximation \(\sin x\sim x\) is used (lines 212-216).
- When \(2^{-26}\leq|x|< 0.855469\text{,}\) \(\sin x\) is approximated by its Taylor polynomial of order 5, evaluated in line 140 via the Horner's method (lines 217-222).
- When \(0.855469\leq|x|<2.426265\text{,}\) \(\sin x\) is evaluated as \(\cos(\pi/2-x)\text{,}\) which is by its Taylor polynomial of order 6, evaluated in line 113 via the Horner's method (lines 224-230).
- When \(2.426265\leq|x|< 105414350\text{,}\) first the angle is brought back, by periodicity, to an angle in the interval \([-\pi/2,\pi/2]\) and then is approximated by the Taylor polynomial of order 5 of either \(\sin x\) or \(\cos x\text{,}\) depending on the initial angle (lines 232-237).
- When \(105414350\leq|x|< 2^{1024}\text{,}\) the same procedure in the point above is followed but a different subroutine is used for reducing the angle by periodicity (lines 239-244).
- When \(|x|>2^{1024}\text{,}\) an overflow error is reported.
How can we verify the accuracy of a function implementation? A way to make sure a function is well implemented is comparing its values with those ontained by any package able to use a higher accuracy. Nowadays there are several of these packages, for instance the GNU MPFR C library or Python's mpmath library. Both libraries are able to perform efficient calculations in arbitrarily large accuracy (provided you have enough RAM for it!). The code below compares the value of NumPy's sine function (in double precision, namely with no more than 17 decimal significant digits) against the values of the mpmath's sine function with 20 decimal significant digits.
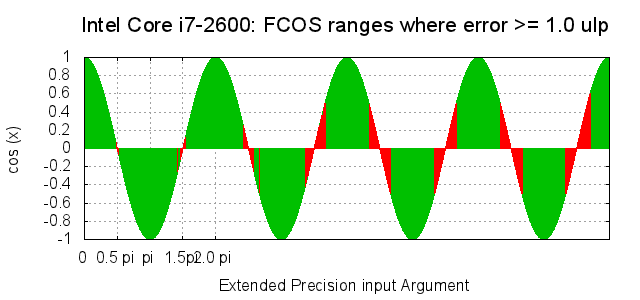
Why not using hardware implementations of functions? Hardware implementations are faster than their software counterpart but have a big drawback: errors cannot be fixed by users as it happens for open-source software packages (among which Python, GCC and MPFR). The unreliability of some hardware implementations is discussed in legth in the following pages:
For instance, the picture below shows, in red, some range where the value of cosine evaluated by a Intel Code i7-2600 CPU differs from the actual cosine value (evaluated by MPFR) by more than 1ulp (unit in the last place), namely with a relative error larger than \(\varepsilon_m\text{.}\)